Расчет поля симметричного распределения зарядов в неоднородной среде по теореме Гаусса

М.И. Векслер, Г.Г. Зегря

Рассмотрим пример сферической системы ρ = ρ(r), кроме того, возможно, имеются заряженные сферы (Ri, σi) и/или точечный заряд qc в центре. Помимо этого, ε = ε(r). Согласно теореме Гаусса,

qinside = 4π r2 Dr = 4π ε0ε(r) r2 Er

(31)

(32)

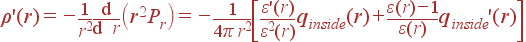
(33)

При наличии только объемного стороннего заряда ρ

(34)

В точках разрыва ε(r) (на стыке двух диэлектриков) или qinside(r) (в момент "перехода" через заряженную сферу) соответствующая производная ε'(r) или qinside'(r) имеет разрыв. При этом поверхностный связанный заряд составляет:

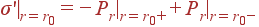
(35)

Другие значения r проверять на наличие связанного заряда бессмысленно, так как там заведомо σ' = 0.

Задача. Имеются две концентрические заряженные сферы (σ1, R1 и σ2, R2). Найти Er(r), φ(r) и σ ', если пространство между сферами заполнено однородным диэлектриком с проницаемостью ε.

Решение Такая задача, только без диэлектрика между обкладками, уже была решена нами с использованием теоремы Гаусса. Единственным отличием здесь будет связь Dr(r) и Er(r) в области R1

Как и раньше,

qinside = 4π r2 Dr(r)

причем

qinside	=	0 при r
		4πσ1R12 при R1
		4πσ1R12+4πσ2R22 при r>R2

Поле на каждом из участков будет

Er	=	0 при r

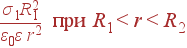
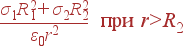
При вычислении потенциала мы должны вычислить 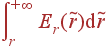. При этом необходимо правильно выписывать Er на каждoм участке:

φ(r)	=
	=
φ(r)	=
	=
φ(r)	=
	=

В некоторых выражениях для φ(r) (но не всюду!) появилась дополнительная величина ε.

Для нахождения σ ' на сферах r = R1 и r = R2 нам потребуются значения поляризованности с обеих сторон каждой из сфер:

	,
	,

Нулевые значения появились из-за отсутствия диэлектрика в областях rR2. Сразу же находим 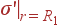и 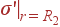(на других поверхностях никакого связанного заряда нет):

	=
	=

Легко проверить, что суммарный связанный заряд, то есть 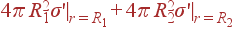, равен нулю, как и должно быть.

Задача. Шар радиуса R равномерно заряжен по объему сторонним зарядом ρ. Проницаемость шара ε. Найти Er(r), φ(r), ρ'(r), σ' на краю шара.

Ответ: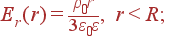

.

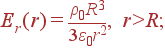
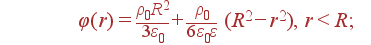
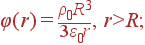
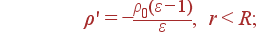
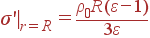1. И.Е. Иродов, Задачи по общей физике, 3-е изд., М.: Издательство БИНОМ, 1998. - 448 с.; или 2-е изд., М.: Наука, 1988. - 416 с.

2. В.В. Батыгин, И.Н. Топтыгин, Сборник задач по электродинамике (под ред. М.М. Бредова), 2-е изд., М.: Наука, 1970. - 503 с.

3. Л.Д. Ландау, Е.М. Лифшиц, Теоретическая физика. т.8 Электродинамика сплошных сред, 2-е изд., М.: Наука, 1992. - 661 с.

Вместе с этим смотрят:

РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора

Актуальные проблемы квантовой механики

Алгебра и алгебраические системы

Анализ эмпирического распределения

Аналитическая теория чисел. L-функция Дирихле