Двойное векторное произведение
Выполнила: ИльенкоВа Ульяна Игоревна, студентка 1 курса, математического факультета
Запорожский национальный университет
Запорожье, 2006 год
Трём векторам a, b и c можно поставить в соответствие вектор, равный a×(b×c). Этот вектор называют двойным векторным произведением векторов a, b и c. Двойное векторное произведение встречается в механике и физике.
Двойное векторное произведение выражается через линейную комбинацию двух или трёх своих сомножителей по формуле
a×(b×c) = b(ac) - c(ab).
Докажем это. Обозначим через x разность левой и правой частей этого равенства
x = a×(b×c) - b(ac) + c(ab).
Нам достаточно показать, что x = 0.
Предположим, что векторы b и c коллинеарны. Если они оба нулевые, то в выражении для вектора x все слагаемые равны нулевому вектору и поэтому равенство
x = 0 выполнено. Если же один из коллинеарных векторов b, c ненулевой, например c, то для другого вектора при некотором α i R выполнено равенство b=αc. Но тогда
x=a×(αc×c)-αc(ac)+cα(ac)=0.
Предположим теперь, что векторы b и c неколлинеарны. Тогда их векторное произведение не равно нулевому вектору и ортогонально ненулевому вектору b. Векторы

образуют правый ортонормированный базис в V3 (это и отражается в обозначениях). В этом базисе справедливы следующие разложения векторов:
b=|b|i , c = c1i+c2k , a = a1i + a2j + a3k ,
и поэтому
b×c = - |b|c2j , a×(b×c) = - |b|c2(a1k тАУ a3i).
Кроме того,
ac = a1c1 тАУ a3c2 , ab = a1|b|.
В результате находим, что и в случае неколлинеарных векторов b и c выполнено равенство
x= -|b|c2(a1k тАУ a3i) тАУ (a1c1 тАУ a3c2)|b|i + a1|b|(c1i + c2k) = 0.
Произведение (a×b)×c ортогонально вектору a×b, то есть в случае, когда векторы a и b не коллинеарны, лежит в плоскости векторов a и b. Следовательно, оно разлагается по векторам a и b, то есть существуют такие два числа x и y, что
(a×b)×c=xa+yb.
Чтобы найти эти числа, мы воспользуемся леммой, согласно которой существуют положительно ориентированный ортонормированный базис е1, е2, е3 ,связанный с векторами a, b и с формулами
a=a1e1
b=b1e1+b2e2,
c=c1e1+c2e2+c3e3.
В этом базисе вектор a×b имеет координаты (0,0, a1b2) , и потому вектор (a×b)×c тАУ координаты
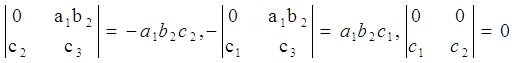
Так как вектор xa+yb имеет координаты (xa1+yb1, yb2, 0), то, следовательно, формула (a×b)×c=xa+yb будет иметь место при
x = -b1c1 тАУ b2c2 , y = a1c1.
Поскольку, с другой стороны, а1с1 = ас и b1c1+b2c2 = bc, этим доказано следующее предложение:
ПРЕДЛОЖЕНИЕ. Для любых векторов a, b, c имеет место равенство (a×b)×c=(ac)b-(bc)a.
Из этой формулы непосредственно вытекает следующее тождество Якоби:
(a×b)×c+(c×a)×b+(b×c)×a=0.
Действительно, в силу коммутативности скалярного умножения
(ac)b-(bc)a+(cb)a-(ab)c+(ba)c-(ca)b=0.
С помощью формулы (a×b)×c=(ac)b-(bc)a легко вычисляется также скалярное произведение (a×b)(x×y) двух векторных произведений. Действительно пользуясь антикоммутативностью смешанного произведения, мы немедленно получим, что
(a×b)(x×y)=((xa)y-(ya)x)b=(xa)(yb)-(ya)(xb),
то есть
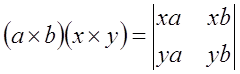
Определитель в правой части этой формулы называется взаимным определителем Грамма пар векторов a,b и x,y.
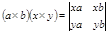 При a=x и b=y формула даёт формулу
При a=x и b=y формула даёт формулу
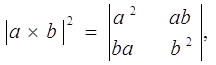
которую можно переписать также в следующем изящном виде:
|a×b|2+|ab|2 = a2 b2.
Определитель в правой части предыдущей формулы называется определителем Грамма пары векторов a и b.
 Поскольку |a×b| равно площади S параллелограмма, построенного на векторах a, b, формула
Поскольку |a×b| равно площади S параллелограмма, построенного на векторах a, b, формула
равносильна формуле
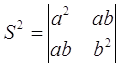
в которой векторные произведения явно не участвуют. Таким образом, мы видим, что определитель Грама пары векторов равен квадрату площади параллелограмма, построенного на этих векторах.
Вычислив скалярные произведения через координаты мы немедленно получим следующее тождество Лагранжа :
 При а3=0 , b3 = 0 (Влслучай плоскостиВ») тождество Лагранжа равносильно тождеству
При а3=0 , b3 = 0 (Влслучай плоскостиВ») тождество Лагранжа равносильно тождеству
(a21+a22)(b21+b22) = (a1b1 + a2b2)2 + (a1b2 тАУ a2b1)2,
Известному из теории комплексных чисел (тождество выражает тот факт, что произведение модулей комплексных чисел a1+ia2 и b1+ib2 равно модулю их произведения).
Аналогом вышеприведённых формулы и тождества существует и для трёх векторов a, b, c. В нём участвует определитель
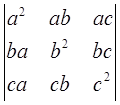
называемый определителем Грамма тройки векторов a, b, c. В координатах относительно ортонормированного базиса e1, e2, e3 , в котором векторы a, b, c выражаются по формулам
a=a1e1
b=b1e1+b2e2,
c=c1e1+c2e2+c3e3 , этот определитель имеет вид
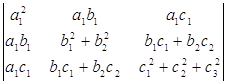
Автоматическое вычисление показывает, что он равен a21b22c23. С другой стороны, как мы уже знаем, a1b2c3= abc. Таким образом
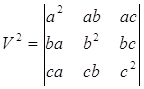
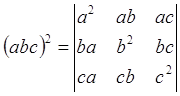
, то есть
где V тАУ объём параллелепипеда, построенного на векторах a, b, c.
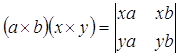
Аналог формулы имеет вид
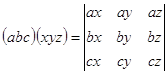
где определитель справа называется взаимным определителем Грама троек a, b, c и x, y, z.
Для подготовки данной работы были использованы материалы с сайта http://referat.ru/
Вместе с этим смотрят:
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
Актуальные проблемы квантовой механики
Алгебра и алгебраические системы
Анализ эмпирического распределения
Аналитическая теория чисел. L-функция Дирихле