Аналогiя: теорема Пiфагора на площинi i в просторi
Змiст
Вступ
Роздiл 1. Теорема Пiфагора на площинi
1.1 Рiзнi доведення теореми Пiфагора
1.2 Теорема Пiфагора та цiлочисловi прямокутнi трикутники
1.3 РЖсторичнi вiдомостi
1.4 РозвтАЩязування задач
Задача 1
Задача 2
Задача 3
Задача 4
Задача 5
Роздiл 2. Теорема Пiфагора у просторi або стереометричний аналог теореми Пiфагора
2.1 Теорема(стереометричний аналог теореми Пiфагора)
Доведення 1
Доведення 2
Доведення 3
Доведення 4
Доведення 5
Доведення 6
Доведення 7
Доведення 8
Доведення 9
Висновок
Лiтература
Вступ
Математик тАУ це той , хто вмii знаходити аналогii мiж твердженнями; кращий математик той, хто встановлюi аналогii доведень; бiльш сильний математик той, хто помiчаi аналогii теорiй; але можна уявити собi й такого, хто мiж аналогiями бачить аналогii. (Стефан Банах)
Аналогiя i таким умовидом, при якому, встановивши схожiсть будови обтАЩiктiв у деяких властивостях, припускають , що вони, можливо, схожi i в iнших властивостях.
Вiдомо, що в процесi розвитку науки висновки за аналогiiю вiдiграють велику роль. Аналогiя, як важлива форма мислення завжди привертала до себе увагу i була предметом дослiдження видатних вчених, мислителiв. Чудовi зразки мiркувань за аналогiiю дали такi вiдомi природодослiдники, як Леонардо да Вiнчi, Й. Кеплер, Г. Галiлей, М.В. Ломоносов, Ч. Дарвiн, Д.РЖ. Менделiiв, К. Максвелл, А. Ейнштейн та iншi. За допомогою аналогii вони обТСрунтували ряд найважливiших наукових вiдкриттiв.
Серед цiнностей iнтелекту Влвищого порядкуВ», що являють собою найважливiшу частину математичноi освiти, одне з прiоритетних мiсць, ймовiрно, займаi вмiння знаходити i застосовувати аналогii. Про цей метод поетично i захоплено говорив Стефан Банах: ВлМатематик тАУ це той, хто вмii знаходити аналогii мiж твердженнями; кращий математик той, хто встановлюi аналогii доведень; бiльш сильний математик той, хто помiчаi аналогii теорiй; але можна уявити собi й такого, хто мiж аналогiями бачить аналогii. В»
Але бiльш багатогранно аналогiя виявляiться у творчiй дiяльностi людини. Велике значення маi аналогiя для творчого мислення.
Аналогiя застосовуiться в учнiвському пiзнаннi
П.М. РДрднiiв вважаi, що володiння ум овидом за аналогiiю Влсприяi як творчостi вченого тАУ математика, так i успiшному навчанню цiii науки або самостiйному вивченню iiВ».
Роль аналогii значно зростаi в сучасних умовах навчання, коли перед школою стоiть завдання озброювати учнiв не лише знаннями, а й методами самостiйного здобуття знань.
Звернемо увагу на основнi дидактичнi функцii аналогii. По-перше, аналогiя сприяi бiльш глибокому осмисленню матерiалу, що вивчаiться. При цьому застосовуiться тi види аналогii, якi конкретизують образи i уявлення. По-друге, аналогiя при вивченнi нового матерiалу допомагаi пiдводити учнiв до визначення нових для них понять, самостiйних пошукiв способу розвтАЩязання задачi, ефективноi органiзацii повторення, узагальнення i систематизацii матерiалу.
Вбачаючи в аналогii великi дидактичнi можливостi, вченi радять користуватись нею i вчителю, i учням. Проте слiд памтАЩятати, що висновки в умовиводах за аналогiiю не даi вiдповiдi на питання про правильнiсть припущення, ця правильнiсть повинна перевiрятись iншими засобами. Та аналогiя важлива вже тим,що вона наводить на здогади, подаi думку про те чи iнше припущення. Це дуже важливо як у розвитку науки, так i в вивченнi математики.
Звiдси випливаi актуальнiсть вибраноi теми.
Об'iкт дослiдження тАУ теорема Пiфагора на площинi i в просторi;
Предмет дослiдження тАУ аналогiя мiж теоремою Пiфагора на площинi i в просторi;
Мета дослiдження тАУ розглянути в чому полягаi аналогiя мiж теоремою Пiфагора на площинi i в просторi.
Для реалiзацii поставленоi мети необхiдно розв'язати наступнi завдання:
- пiдiбрати, опрацювати та систематизувати лiтературнi джерела з обраноi теми;
- пiдiбрати, класифiкувати та зiбрати задачi про теорему Пiфагора на площинi i в просторi (на доведення та обчислення).
Курсова робота складаiться зi вступу, двох роздiлiв,висновку,списку використаноi лiтератури, що мiстить 3 найменування.
У вступi визначаiться об'iкт, предмет,мета та завдання дослiдження, обТСрунтовуiться актуальнiсть обраноi теми,описана структура курсовоi роботи.
В наступних роздiлах йде огляд i доведення аналогii мiж трикутником та тетраедром. У висновку пiдведено пiдсумок про виконану роботу.
Роздiл 1. Теорема Пiфагора на площинi
Теорема Пiфагора. У прямокутному трикутнику квадрат довжини гiпотенузи дорiвнюi сумi квадратiв довжини катетiв.
Дано: ΔАВС,  С = 90В°, ВС = а, АС = b, АВ = с.
С = 90В°, ВС = а, АС = b, АВ = с.
Довести: с2 = а2 + b2
1.1 Рiзнi доведення теореми Пiфагора
Доведення 1. На гiпотенузi i катетах побудуiмо квадрати i виконаiмо додатковi побудови, якi видно на рисунку 1. Тодi  NAB = 90В° +
NAB = 90В° +  САВ,
САВ,
 САЕ =90В° +
САЕ =90В° +  САВ. Отже,
САВ. Отже,  NАВ =
NАВ =  САЕ. Крiм цього, NА = СА, АВ = АЕ.
САЕ. Крiм цього, NА = СА, АВ = АЕ.
Таким чином, за першою ознакою рiвностi трикутникiв маiмо: ΔNAB = ΔCAE. Але SΔNAB= 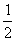 NAВ·NK =
NAВ·NK = 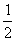 SΔANRC, SΔCAE=
SΔANRC, SΔCAE= 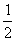 AEВ·EH =
AEВ·EH = 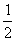 SAEHR. Порiвнюючи останнi три рiвностi, дiстанемо: SANKC= SAEHR. ( 1 ) Аналогiчно,
SAEHR. Порiвнюючи останнi три рiвностi, дiстанемо: SANKC= SAEHR. ( 1 ) Аналогiчно,  ВаABE = 90В° +
ВаABE = 90В° +  ABC,
ABC,  CBD = 90В° +
CBD = 90В° +  ABC. Звiдси
ABC. Звiдси  ABF =
ABF =  CBD. Крiм того, AB тАУ DB, CB тАУ FB. Тодi за першою ознакою рiвностi трикутникiв ΔABF = ΔDBC. Але SΔABF =
CBD. Крiм того, AB тАУ DB, CB тАУ FB. Тодi за першою ознакою рiвностi трикутникiв ΔABF = ΔDBC. Але SΔABF = 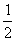 BFВ·QF =
BFВ·QF = 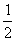 SBCQF, SΔDBC =
SBCQF, SΔDBC = 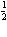 BDВ·HD =
BDВ·HD = 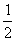 SHRBD. З цих рiвностей одержимо: SBCQA = SHRBD. ( 2 ) Додамо почленно рiвностi (1) i (2):
SHRBD. З цих рiвностей одержимо: SBCQA = SHRBD. ( 2 ) Додамо почленно рiвностi (1) i (2):
SANKC + SBCQF = SAEHR + SHRBD, але SAEHR + SHRBD = SAEDB.
Таким чином, SANKC + SAEDB або b2 + a2 = c2
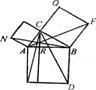
Рис. 1
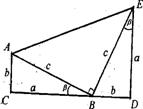
Рис. 2
Доведення 2
Побудуiмо ΔBDE = ΔACB так, щоб B 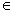 ВаCD ( рис 2).
ВаCD ( рис 2).
Тодi чотирикутник ACDE тАУ трапецiя, бо AC || DE як два перпендикуляри до CD. Маiмо:
SACDE= 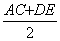 В·CD =
В·CD = 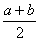 В·
В·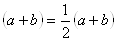 2 (1)
2 (1)
Крiм того, SACDE= SΔABE + 2SΔABC. Трикутник ABE рiвнобедрений i прямокутний. Дiйсно, якщо позначимо  АВС =
АВС =  BED =
BED = 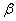 , тодi в прямокутному трикутнику BDE
, тодi в прямокутному трикутнику BDE  DBE = 90В° -
DBE = 90В° - 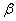 . За побудовою
. За побудовою  CBD = 90В°.Таким чином,
CBD = 90В°.Таким чином,  ABE = 180В° -
ABE = 180В° - 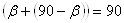 В°, SΔABC=
В°, SΔABC=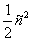 , SΔABC=
, SΔABC= 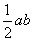 .
.
Тодi SACDE= 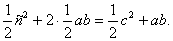 Ва( 2 )
Ва( 2 )
Порiвнюючи рiвностi ( 1 ) i ( 2 ), дiстанемо:
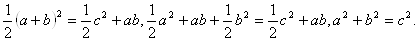
Доведення 3. Побудуiмо CD 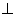 ВаAB ( рис.3 ).
ВаAB ( рис.3 ).
Нехай  CAB =
CAB =  BCD =
BCD = 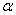 . Тодi SΔABC =
. Тодi SΔABC = 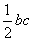 sin
sin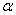 . Оскiльки
. Оскiльки 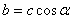 ,
,
SΔABC = 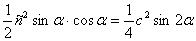 Ва( 1 )
Ва( 1 )
Аналогiчно: SΔACD= 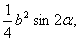 Ва( 2 )
Ва( 2 )
SΔBCD= 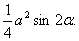 Ва( 3 )
Ва( 3 )
За побудовою SΔABC= SΔACD+ SΔBCD. ( 4 )
З рiвностей ( 1 ), ( 2 ), ( 3 ), ( 4 ) випливаi:

тобто 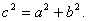
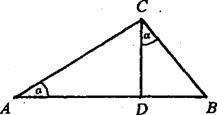 Рис.3
Рис.3 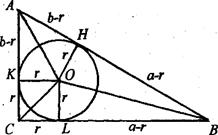 ВаРис.4
ВаРис.4
Доведення 4. Впишемо в трикутник АВС коло ( О, r ) ( Рис.4 ). Тодi:
SΔABC= SΔOAC + SΔOAB = 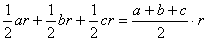
Чотирикутник OKCL тАУ квадрат з стороною r. За властивiстю дотичних, проведених з точок А та В до кола, маiмо: AH = AK = 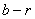 , BH = BL =
, BH = BL = 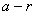 .
.
Тодi
AB = AH + HB = 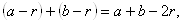

З iншого боку
SΔABC = 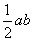 .
.
Таким чином,
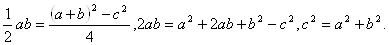
Доведення 5
Виконуiмо побудови, якi показано на рисунку 5 а), 5 б).
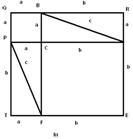
Рис.5,а
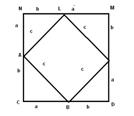
Рис.5,б
CDMN, TQRE тАУ квадрати зi стороною 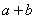 . Тодi SCDMN = STQRE.
. Тодi SCDMN = STQRE.
За побудовою маiмо:
SCDMN= SABLK + 4SΔABC,
STQRE = SPQBC+ SACFE + 4SΔABC.
Порiвнюючи цi рiвностi, дiстанемо:
SABLK+ 4SΔABC= SPQBC+ SACFE + 4SΔABC, або
SABLK = SPQBC+ SACFE, тобто 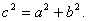
Доведення 6
Побудуiмо квадрат CDMN з стороною a+b ( Рис.6)
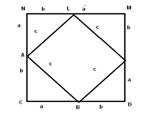
Рис. 6
Тодi ΔАСВ = ΔBDK = ΔKLM = ΔLNA ( за двома катетами ) , звiдки
AB = BK = KL = LA = c.
Отже, чотирикутник ABKL тАУ ромб.
Оскiльки  АВК = 90В°, то ABKL тАУ квадрат. Маiмо:
АВК = 90В°, то ABKL тАУ квадрат. Маiмо:
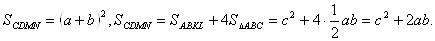
Порiвнюючи останнi рiвностi, дiстанемо:
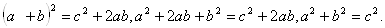
Доведення 7
На сторонах прямокутного трикутника АВС побудуiмо квадрати АВКМ, АDЕС, ВСFR. (Pис. 7). Трикутники ЕСF, КLМ i АСВ рiвнi мiж собою. АDRВ = EDRF як симетричнi вiдносно прямоi DR фiгури; ACLM = КLСВ як центрально-симетричнi фiгури вiдносно центра квадрата АВКМ; АDRB=АСLМ як вiдповiднi фiгури при поворотi навколо центра А на кут 90В°.
Враховуючи одержанi три рiвностi, маiмо:
ADEFRB = ACBKLM, але
SADEFRB= SADEC+ 2SΔABC + SBCFR, SACBKLM = SABKM + 2SΔABC.
Отже, SADEC+ SBCFR = SABKM, тобто 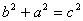
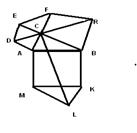



 Рис.7
Рис.7
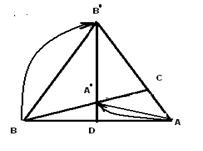
Рис.8
Доведення 8
Прямокутний трикутник АСВ з прямим кутом С повернемо навколо точки С на 90В° так, щоб вiн зайняв положення А´СВ´ ( Рис. 8 ).Продовжимо гiпотенузу А´В´ до перетину з АВ у точцi D. Вiдрiзок В´D буде висотою трикутника В´АВ.
Розглянемо тепер чотирикутник А´АВ´В. Його можна розкласти на два рiвнобедренi трикутники СА´А i СВ´В. Маiмо:
ЫΔi´Ф = 
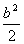 б ЫΔСИ´И=
б ЫΔСИ´И= 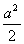 ю
ю
Таким чином
ЫФ´ФИ´И= ЫΔi´Ф + ЫΔСИ´И=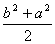 ю
ю
Трикутники АА´В´ i ВА´В´ мають спiльну основу В´А´ i висоти AD i BD вiдповiдно. Тому
ЫФ´ФИ´И= ЫΔАФ´В´ + ЫΔВА´И= 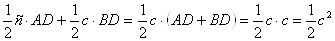 ю
ю
Порiвнявши два вирази для площi чотирикутника А´АВ´В, одержимо:
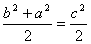 , тобто
, тобто 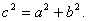
1.2 Теорема Пiфагора та цiлочисловi прямокутнi трикутники
Спiввiдношення мiж сторонами прямокутного трикутника, яке подаiться в пiдручниках математики та iнших джерелах пiд назвою теореми Пiфагора, було вiдоме з давнiх часiв. Так, клинописi пам'ятки Вавiлона свiдчать про те, що за 2-2,5 тисячi рокiв до нашоi ери там уже користувалися названим спiввiдношенням для обчислень. Було вiдоме воно i стародавнiм iгиптянам (за 2300 рокiв до н.е.) ,про що свiдчить папiрус Берлiнського музею. Чому ж ця закономiрнiсть названа iм'ям Пiфагора, який жив у VI cт. до н.е., тобто значно пiзнiше?
Пiфагор, про життя якого i лише вiдомостi, переписанi легендами, народився на о. Самос. У молодi роки вiн багато подорожував i цiлком iмовiрно, що, вiдвiдавши краiни Стародавнього Сходу, познайомився з вiдомою вже там закономiрнiстю про спiввiдношення мiж сторонами прямокутного трикутника. Повернувшись на батькiвщину (в Грецiю) та оселившись у м. Кротонi, Пiфагор заснував фiлософську школу i серйозно зайнявся систематизацiiю та узагальненням математичних знань. Пiфагор систематизував здобутi фрагментарнi вiдомостi про прямокутний трикутник, дав iм логiчне обТСрунтування, зробивши iх надбанням своiх спiввiтчизникiв.
Першопрохiдцi помiтили, що рiвнiсть a2+b2=c2 (1) справджуiться при натуральних значеннях довжин катетiв а i b та гiпотенузи с, бо iнших чисел вони не знали.
ЗтАЩясуiмо насамперед, чи i такi три послiдовностi натуральних чисел, що задовольняють рiвнiсть (1). Якщо i, то скiльки таких трiйок чисел?
Нехай a=n -1; b=n ; c=n+1. Тодi (n -1)2+ n2 =( n +1)2 , звiдки n2-4n=0; n1=0; n2=4. Умову задачi задовольняi n=4.
Отже, маiмо трiйку чисел 3,4,5, для яких 32+42=5 2.Оскiльки iнших розвтАЩязкiв рiвняння не маi, то iснуi лише одна така трiйка чисел.
Прямокутний трикутник зi сторонами 3, 4 i 5 був вiдомий стародавнiм iгиптянам. Ним вони користувалися, будуючи прямi кути пiд час землевимiрювальних робiт. Подiливши вiрьовку на 12 рiвних частин, закрiплювали ii кiлками в подiлках, якi вiд одного кiнця вiддiляли 3 вiдрiзки, а вiд другого тАУ 5. Натягуючи вiльнi кiнцi вiрьовки та сумiщаючи iх, дiставали прямокутний трикутник з прямим кутом мiж вiдрiзками 3 i 4 одиницi. Людей, якi займалися цiiю справою, називали гарпедонаптами (натягувачi вiрьовок), а прямокутний трикутник зi сторонами 3, 4, i 5 дiстав назву iгипетського.
Назвемо прямокутнi трикутники довжини сторiн яких виражаються цiлими числами, цiлочисловими. Зрозумiло, що трикутники зi сторонами 3k, 4k i 5k прямокутнi цiлочисловi, бо (3k)2+(4k)2=(5k)2 ↔ 32+42=5 2. Таких трикутникiв безлiч.
Чи iснують цiлочисловi прямокутнi трикутники, крiм iгипетського, довжини сторiн яких тАУ три числа, що мають найбiльшим спiльним дiльником число 1? Шукатимемо такi трикутники, тобто такi трiйки натуральних чисел, якi задовольнятимуть зазначену вище умову. Виходячи з умови, вони не можуть бути всi парними, але не можуть бути й не парними,бо , якщо a i b непарнi, то с парне. (Зазначимо тут, що коли, наприклад, a парне, то a2 кратне 4, бо якщо a=2п ,то a2=4п2.Якщо a непарне, тобто a=2п+1, то a2=4п2+4п+1=4п1+1 тАУ непарне).
Взагалi, якщо будь-якi два числа з трiйки натуральних чисел a, b i c ,що задовольняють a2+b2=c2 (такi числа називають пiфагоровими), мають спiльний дiльник вiдмiнний вiд 1, то вiн буде також дiльником i третього числа. Отже, будь-яка пара чисел з шуканих трiйок i взаiмно-простими числами. Нехай aнепарне i bпарне, тодi c також непарне.
Маiмо :
a2+b2=c2 ↔ b2=c2- a2↔ b2=(c-a)(c+a).(2)
Числа (c-a) i (c+a) парнi, тому тому 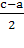 Ваi
Ваi 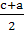 Вацiлi ; b2 кратне 4, тому
Вацiлi ; b2 кратне 4, тому 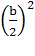 Вацiле .З рiвностi ( 2 ) дiстанемо:
Вацiле .З рiвностi ( 2 ) дiстанемо:
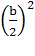 =
=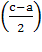 Ва*
Ва* 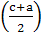 Ва(3).
Ва(3).
Числа 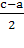 Ваi
Ваi 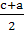 Вавзаiмно простi. Справдi, якщо припустити протилежне, то
Вавзаiмно простi. Справдi, якщо припустити протилежне, то
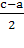 =ир1 i
=ир1 i 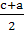 Ва=ир2.
Ва=ир2.
Отже
С = и (р1+р2) i а = и (р1-р2),
тобто числа с i а матимуть спiльний дiльник и, що суперечить умовi.
Добуток двох взаiмно простих чисел i точним квадратом (рiвнiсть 3) лише в тому випадку, коли кожне з цих чисел i точним квадратом. Нехай
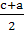 Ва=х2;
Ва=х2; 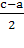 =у2, тодi с=х2+у2 ; а=х2-у2 i
=у2, тодi с=х2+у2 ; а=х2-у2 i 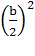 =х2у2, або
=х2у2, або 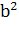 =(2ху)2; b=2ху.
=(2ху)2; b=2ху.
Маiмо тотожнiсть
(х2-у2)2+(2ху)2=(х2+у2)2.
Формули
а=х2-у2; b=2ху i с=х2+у2
дають можливiсть обчислювати a, b i c за значеннями х i у.
Якщо числа х i у взаiмно простi й до того ж одне з них парне, а друге непарне, то трiйки (a,b,c) будуть саме такi, як у вихiднiй задачi(найбiльший спiльний дiльник a, b, c дорiвнюi 1) . Такi трiйки пiфагорових чисел називаються основними.
Основнi трiйки пiфагорових чисел модна дiстати, склавши таку таблицю.
| х | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| у | 1 | 2 | 1 | 3 | 2 | 1 | 1 | 5 | 2 | 4 | 6 | 1 | 3 | 5 | 7 |
a=x2-y2 b=2xy c=x2+y2 | 3 4 5 | 5 12 12 | 15 8 17 | 7 24 25 | 21 20 29 | 9 40 41 | 35 12 37 | 11 60 61 | 45 28 53 | 33 56 65 | 13 84 85 | 63 16 65 | 55 48 73 | 39 80 89 | 15 112 113 |
РЗi можна продовжити як завгодно довго. Отже, таких трiйок чисел безлiч.
РДгипетський трикутник, як видно з таблицi, дiстанемо, якщо х=2, у=1. Помiчаiмо також, що коли х-у=1, гiпотенуза бiльша вiд бiльшого катета на 1. Це природно, бо коли
х=у+1, b=2xy=2у(у+1)=2у2+2у; с=(у+1)2+у2=2у2+2у+1 i тому с- b=1.
При цьому менший катет а=х2-у2=2у+1, а рiзниця довжин катетiв b-а=2у2-1.Цей вираз дорiвнюi 1 тiльки тодi, коли у=1. Знову приходимо до висновку, що iснуi лише один прямокутний трикутник, довжини сторiн якого виражаються трьома послiдовними натуральними числами.
Сума довжин гiпотенузи й катета b i точний квадрат, бо
с+b=х2+у2+2ху=(х+у)2.
Точним квадратом i також i iх рiзниця, тобто
с-b=х2+у2-2ху=(х-у)2.
Якщо х-у=п, то с-b=п2. Наприклад, якщо х=5 i у=2, маiмо b=20 i с=29;
х+у=7; b+с=20+29=49=72; с- b=29-20=9=32.
Зрозумiло,що з кожноi основноi трiйки пiфагорових чисел модна дiстати безлiч похiдних, бо
a2+b2=c2↔(3а)2+(4b)2=(5с)2
Наприклад, маючи трiйку (3;4;5), дiстанемо трiйки (6;8;10), (9;12;15), (12;16;20) та iн.
До речi, усi трiйки пiфагорових чисел, якi походять вiд основноi трiйки (3;4;5), i основна трiйка i арифметичними прогресiями. РЖнших трiйок пiфагорових чисел, якi б були арифметичними прогресiями немаi.
Неважко показати, що серед основних трiйок(а отже, i похiдних) немаi жодноi, яка була б геометричною прогресiiю.
Припустимо, то така трiйка (а;b;с) iснуi. Тодi b2=ас i значить а2+ас=с2. Звiдси ас=с2-а2, або ас=(с+а)(с-а). Числа а i с непарнi, тодi як (с+а) i (с-а) парнi. Отже рiвнiсть, хибна, а це означаi, що зроблене неправильне припущення.
Похiднi трiйки можна дiстати також, надаючи х i у цiлих значень(крiм тих, при яких дiстанемо основнi трiйки) або коли 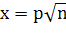 Ваi
Ваi 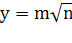 ВаНаприклад, якщо х=4 i у=2, то а=12; b=16; i c=20. Такий результат можна дiстати, помножаючи числа 3, 4 i 5 на 4.Якщо
ВаНаприклад, якщо х=4 i у=2, то а=12; b=16; i c=20. Такий результат можна дiстати, помножаючи числа 3, 4 i 5 на 4.Якщо 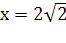 Ваi
Ваi 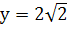 , то а=6, b=8 i с=10; це можна також дiстати, помноживши на 2 числа 3, 4 i 5.
, то а=6, b=8 i с=10; це можна також дiстати, помноживши на 2 числа 3, 4 i 5.
Якщо, наприклад, х=1000 i у=999, то дiстанемо основну трiйку
а=х+у=1999, b=1998000 i с= b+1=1998001.
1.3 РЖсторичнi вiдомостi
Пiфагор Самосський (бл. 580тАУ500 р.р. до н. е.) тАУ давньогрецький математик i фiлософ. Народився на островi Самос в багатiй купецькiй сiмтАЩi, здобув ТСрунтовану освiту. За переказами, Пiфагор для ознайомлення з мудрiстю схiдних учених виiхав до РДгипту i, нiбито, прожив там 22 роки, пiсля чого провiв 12 рокiв у Вавiлонi, де вивчив науковi працi вавiлонських жерцiв. Близько 530 р. до н. е. повернувся на батькiвщину i оселився в мiстi Кротонi. Тут йому вдалося органiзувати власну школу, яка дiяла майже 30 рокiв i здобула велику популярнiсть. Школа Пiфагора багато зробила для перетворення геометрii в науку. Характерною рисою методу Пiфагора було поiднання геометрii з арифметикою: вiдрiзки вiдiгравали роль, аналогiчну тому, як букви в сучаснiй алгебрi. Пiфагор багато займався пропорцiями та прогресiями. Вчення Пiфагора та його учнiв стосувалося гармонii, геометрii, теорii чисел, астрономii тощо. Пiфагорiйцi понад усе цiнували результати, здобутi в теорii гармонii, бо саме тут пiдтверджувалась iхня iдея, що числа визначають все.
Пiфагор один з перших вважав, що Земля маi форму кулi i центром Всесвiту, що сонце, Мiсяць i планети мають власний рух, вiдмiнний вiд добового руху нерухомих зiрок. Цi погляди передували гелiоцентричному вченню Копернiка.
Пiфагору приписують доведення теореми, яка маi його iмтАЩя. РЗi iсторiя оповита легендами. Виявляiться, що вона ще до Пiфагора була вiдома iгиптянам, вавiлонянам, китайцям та iндiйцям.
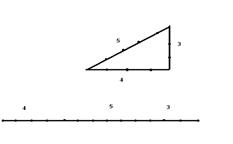
Рис.1
Нiмецький iсторик мате математики Кантор вважаi, що рiвнiсть 32 + 42 = 52 була вiдома iгиптянам ще близько 2300 р. до н. е. в часи царя Аменетхета Ι. На думку Кантора, гарпедонапти, або "натягувачi вiрьовок", будували прямi кути за допомогою прямокутних трикутникiв зi сторонами 3, 4, 5. Можна легко вiдновити iх спосiб побудови. Вiзьмемо вiрьовку довжиною 12м i привтАЩяжемо до неi кольоровi стрiчки на вiдстанi 3м вiд одного кiнця i 4м вiд другого (рис.1). Потiм натягнемо вiрьовку так, як це вказано на рисунку. Прямий кут буде мiж сторонами довжиною в 3 i 4 метри.
Близько 2000 р. до н. е. вавiлоняни вмiли робити окремi обчислення з прямокутними трикутниками.
Геометрiя в iндусiв, як i в iгиптян, була тiсно повтАЩязана з культом. Цiлком ймовiрно, що теорема про квадрат гiпотенузи була вiдома в РЖндii близько 8 ст. до н.е.
Властивостi трикутника з сторонами 3, 4, 5 були вiдомi в Китаi за 1100 р. до н. е., про що засвiдчуi математична книга Чупей.
Теорема Пiфагора маi рiзнi формулювання. В "Початках" Евклiда вона формулюiться так: У прямокутному трикутнику квадрат сторони, натягнутоi над кутом, дорiвнюi квадратам на сторонах, що утворюють прямий кут.
Латинський переклад арабського тексту: У всякому прямокутному трикутнику квадрат, утворений на сторонi, натягнутiй над прямим кутом, дорiвнюi сумi двох квадратiв, утворених на двох сторонах, що замикають прямий кут.
У перекладi з нiмецького читаiться так: Площа квадрата, вимiряна довгою стороною трикутника, настiльки ж велика, як у двох квадратiв, якi вимiрянi двома сторонами його, що прилягають до прямого кута. У першому росiйському перекладi евклiдових "Початкiв", зроблено з грецькоi Ф.РЖ. Петрушевським у 1819 роцi, теорема Пiфагора викладена так: У прямокутних трикутниках квадрат iз сторони, протилежноi прямому куту, дорiвнюi сумi квадратiв iз сторiн, що мiстять прямий кут.
У Францii i деяких областях Нiмеччини теорему Пiфагора називали "мостом ослiв". Вважають, що вона формулювалась так: Квадрат, побудований на гiпотенузi прямокутного трикутника, рiвновеликий сумi квадратiв, побудованих на його катетах.
В епоху середньовiччя теорема Пiфагора визначала границi математичних знань. Характерне креслення теореми Пiфагора використовувалось як символ математики, перетворювалось школярами в карикатури.
Нинi всi погоджуються з тим, що ця теорема не була вiдкрита Пiфагором. Однак, однi вважають, що Пiфагор першим дав ii повноцiнне доведення, iншi вiдомляють йому в цiй заслузi. Дехто приписуi йому доведення, яке Евклiд (жив близько 300 р. до н.е. в Олександрii) наводить у першiй книзi своiх "Початкiв". Проте Прокл, який жив у 410 тАУ 485 р. р. у Вiзантii i Афiнах, стверджуi, що доведення в "Початках" належать самому Евклiду. Вiдомий голандський математик Ван-дер-Варден прийшов до висновку: "Заслугою перших грецьких математикiв, таких, як Фалес, Пiфагор i пiфагорiйцi, i не вiдкриття математики, а ii систематизацiя i обТСрунтування. В iх руках обчислювальнi рецепти перетворились в точну науку".
1.4 РозвтАЩязування задач
Задача 1
Основа трикутника дорiвнюi 40 см. До неi проведенi висота довжиною 12 см i медiана довжиною 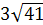 Васм. Обчислити периметр трикутника.
Васм. Обчислити периметр трикутника.
РозвтАЩязання
Нехай у трикутнику АВС, АВ=40см, висота СН=12 см, медiана СМ= 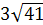 Васм(рис.1)
Васм(рис.1)
З трикутника МНС(Н=90о):
МН=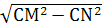 =
=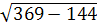 =15(см).
=15(см).
Крiм того, точка Н лежить мiж точками М i В. Оскiльки
МВ = 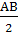 =20(см), то
=20(см), то
НВ=МВ-МН=5(см) i АН=АВ-НВ=35(см).
З 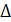 СНВ(Н=90о): СВ=
СНВ(Н=90о): СВ=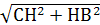 =
=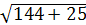 =13(см).
=13(см).
З 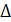 СНА(Н=90о): СВ=
СНА(Н=90о): СВ=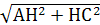 =
=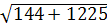 =37(см).
=37(см).
Отже Р=АВ+ВС+АС=40+13+37=90(см.)
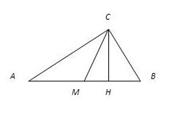
Рис. 1
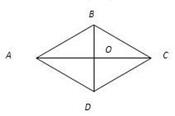
Рис. 2
Задача2
Периметр ромба дорiвнюi 100 см, а дiагоналi вiдносяться як 3:4. Обчислити площу ромба.
РозвтАЩязання
Нехай АВСD тАУ ромб, у якому ВD:АС=3:4 i Р=100(см) (рис.2)
Оскiльки Р=4*АD, то АD=25 см. Враховуючи, що
ВD=2*ОD, АС=2*АО,
Одержимо
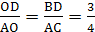 ,
,
звiдки
ОD=3k, AO=4k(k>0).
З 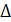 AOD(O=90o): AD2=AO2+OD2, 25=16k2+9k2.
AOD(O=90o): AD2=AO2+OD2, 25=16k2+9k2.
Тодi OD=3*5=15 (см),
АО=4*5=20(см),
SABCD=4*SAOD=4* *AO*OD=2*20*15=600(см2).
*AO*OD=2*20*15=600(см2).
Задача3 (задача Леонардо Фiбоначчi)
Двi башти висотою 30 i 40 футiв розташованi одна проти другоi на вiдстанi 50 футiв одна вiд одноi. Мiж ними знаходиться фонтан, до якого з обох башт злiтають два птахи, i , пролiтаючи з однаковою швидкiстю, прилiтають до фонтану в один i той же час. Яка вiдстань по горизонталi вiддiляi фонтан вiд обох башт(рис.3)?
РозвтАЩязання
Позначимо АЕ=х, тодi DЕ=50-х. З прямокутних трикутникiв ВАЕ i СDЕ за теоремою Пiфагора маiмо : ВЕ2=АЕ2+АВ2, СЕ2=DЕ2+DС2.За умовою ВЕ=ЕС, тодi маiмо АЕ2+АВ2= DЕ2+DС2, х2+402=(50-х)2+302, х2+1600=2500-100х+х2+900, 100х=1800, х=18, DЕ=50-18=32. Отже, АЕ=18 футiв, DЕ=32 фути.
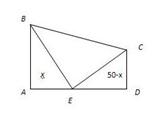
Рис. 3
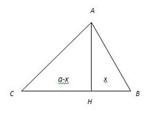
Рис.4.1
Задача 4
Обчислити довжину висоти трикутника, якщо вiдомо довжини його сторiн.
Розв'язання
Нехай ΔАВС, АВ = с, АС = 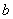 ,ВС = а, АН- висота.Позначимо проекцiю сторони АВ на пряму ВС через
,ВС = а, АН- висота.Позначимо проекцiю сторони АВ на пряму ВС через 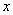 ВаТодi проекцiя сторони АС на що саму пряму буде або а - х (рис. 4.1), або а + х (рис4.2). За теоремою Пiфагора в першому випадку
ВаТодi проекцiя сторони АС на що саму пряму буде або а - х (рис. 4.1), або а + х (рис4.2). За теоремою Пiфагора в першому випадку
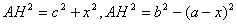
Дiстанемо рiвняння
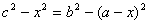
РозвтАЩязуючи його, одержимо:
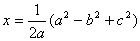
Тодi
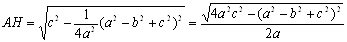
У другому випадку вiдповiдь буде та сама
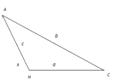
Рис. 4.2
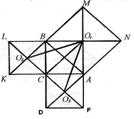
Рис. 5
Задача 5
На сторонах рiвнобедреного прямокутного трикутника з катетом 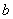 Вапобудованi квадрати зовнi трикутника. Центри цих квадратiв з'iднанi мiж собою прямими лiнiями. Знайти площу одержаного трикутника.
Вапобудованi квадрати зовнi трикутника. Центри цих квадратiв з'iднанi мiж собою прямими лiнiями. Знайти площу одержаного трикутника.
Розв'язання
Нехай
ΔАВС,  C = 90В°, АС = ВС = b,
C = 90В°, АС = ВС = b,
ABMN,ACDF, BCKL - квадрати
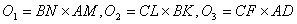
Неважко переконатись в тому, що ΔO1O2O3 тАУ рiвнобедрений, O1C тАУ висота (рис.5).
Тодi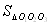 .
.
За теоремою Пiфагора
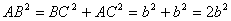
Таким чином,
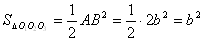
Роздiл 2. Теорема Пiфагора у просторi або стереометричний аналог теореми Пiфагора
Метод аналогii i одним з ефективних i розповсюджених методiв математики. Його застосування приводить до плiдних i часто до неочiкуваних результатiв.
Деякi властивостi трикутника i тетраедра схожi, а деякi геометричнi поняття, повтАЩязанi з трикутником , мають просторовi аналоги: наприклад, сторона трикутника тАУ грань тетраедра, довжина сторони тАУ площа гранi, вписане коло тАУ вписана сфера, площа тАУ обтАЩiм,бiсектриса кута тАУ бiсектор двогранного кута тощо. Багато теорем про трикутники, якщо замiнити в iх формулюваннi планiметричнi термiни вiдповiдними стереометричними i конкретно сформулювати, то вони перетворюються в теореми про тетраедри. Однiiю з таких i аналог теореми Пiфагора в стереометрii.
Означення. Якщо три ребра, якi виходять з однiii вершини тетраедра, попарно ортогональнi, то тригранний кут, що визначаiться ними, називаiться прямим, а тетраедр тАУ прямокутним.
Теорема (стереометричний аналог теореми Пiфагора).У прямокутному тетраедрi квадрат площi гранi, що лежить проти прямого тригранного кута, дорiвнюi сумi квадратiв площ решти граней.
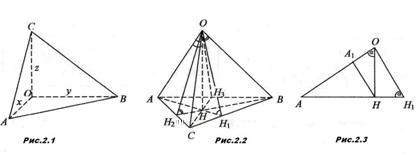
Доведення 1. Нехай у прямокутному тетраедрi OABC
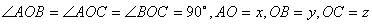 Ва(Рис.2.1)
Ва(Рис.2.1)
Доведемо, що
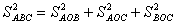
Маiмо:
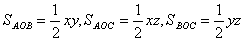 Ва(1)
Ва(1)
У Δ АВС:
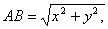
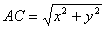 ,
, 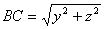 Ва(2)
Ва(2)
Площу трикутника АВС обчислимо за формою Герона
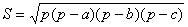 , де
, де 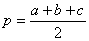
Виконаiмо перетворення:
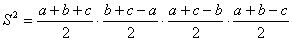 ,
,
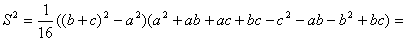
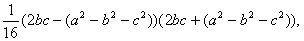
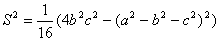 .
.
Використовуючи (2), (3), одержимо:
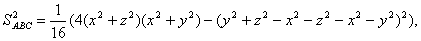
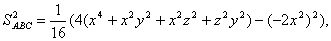
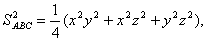
тобто 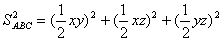 (4)
(4)
Враховуючи (1), (4), одержимо
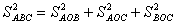
Розглянемо доведення, в якому використовуiться метод проекцiй
Доведення 2
Нехай у прямокутному тетраедрi ОАВС гранi ОВС, ОАС, ОАВ утворюють з основою АВС кути 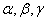 Вавiдповiдно. Оскiльки точка О проектуiться в ортоцентр Н трикутника АВС, то лiнiйнi кути двогранних кутiв при основi утворюватимуться висотами вiдповiдних граней:
Вавiдповiдно. Оскiльки точка О проектуiться в ортоцентр Н трикутника АВС, то лiнiйнi кути двогранних кутiв при основi утворюватимуться висотами вiдповiдних граней: 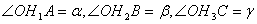 (Рис. 2.2 ).Спроектуiмо висоту ОН на ребра прямого тригранного кута, одержимо: ОА1=ОН
(Рис. 2.2 ).Спроектуiмо висоту ОН на ребра прямого тригранного кута, одержимо: ОА1=ОН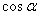 (Рис. 2.3), аналогiчно ОВ1=ОН
(Рис. 2.3), аналогiчно ОВ1=ОН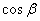 , OC1=OH
, OC1=OH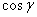 .
.
У прямокутному паралелепiпедi з дiагоналлю ОН i ребрами ОА1, ОВ1, ОС1 справджуiться рiвнiсть
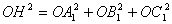
або 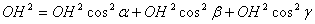 ,
,
звiдки 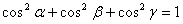 Ва(1)
Ва(1)
Оскiльки 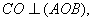 то ΔAOB тАУ ортогональна проекцiя ΔАВС, аналогiчно ΔAOC тАУ ортогональна проекцiя ΔАВС i ΔBOС тАУ ортогональна проекцiя ΔАВС.
то ΔAOB тАУ ортогональна проекцiя ΔАВС, аналогiчно ΔAOC тАУ ортогональна проекцiя ΔАВС i ΔBOС тАУ ортогональна проекцiя ΔАВС.
Маiмо:
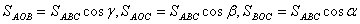 ,
,
звiдси 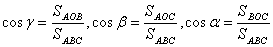 . (2)
. (2)
Враховуючи (1) i (2), одержимо:
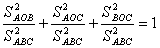 , або
, або 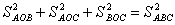 .
.
Пропонуiмо iншi доведення теореми Пiфагора для прямокутного тетраедра.
Доведення 3
Нехай у прямокутному тетраедрi ОАВС
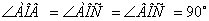 ,
, 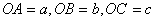 (Рис. 2.4).
(Рис. 2.4).
Побудуiмо висоту СН трикутника АВС i сполучимо точки О i Н.
Маiмо: СН тАУ похила, ОН тАУ ii проекцiя, СН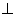 АВ. За теоремою про три перпендикуляри ОН
АВ. За теоремою про три перпендикуляри ОН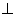 АВ. Знайдемо площу трикутника АВС:
АВ. Знайдемо площу трикутника АВС:
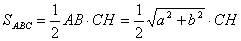
З ΔСОН ( О = 90В° )
О = 90В° ) 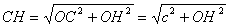 Ва(2)
Ва(2)
Знайдемо ОН, для цього виразимо площу трикутника АОВ через катети, тобто
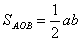 (3),
(3),
теорема пiфагор площина простiр
i через гiпотенузу АВ та висоту ОН, опущену на неi, тобто
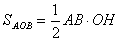
або 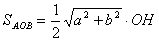 (4)
(4)
З рiвностей (3), (4)
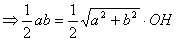 ,
,
звiдки 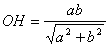 . (5)
. (5)
Враховуючи ( 2 ), ( 5 ), одержимо:
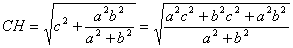 (6)
(6)
Спосiб 1. Враховуючи ( 1 ), ( 6 ) одержимо:
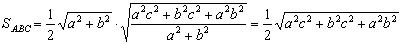
Тод
Вместе с этим смотрят:
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
Актуальные проблемы квантовой механики
Алгебра и алгебраические системы
Анализ эмпирического распределения
Аналитическая теория чисел. L-функция Дирихле