Застосування частинних похiдних

ЗАСТОСУВАННЯ ЧАСТИННИХ ПОХРЖДНИХ

1. Дотична площина та нормаль до поверхнi. Геометричний змiст диференцiала функцii двох змiнних

Нехай задано поверхню

. (1)

Точка Ваналежить цiй поверхнi i функцiя Вадиференцiйована в точцi , причому не всi частиннi похiднi в точцi Вадорiвнюють нулю, тобто

.

Розглянемо довiльну криву, яка проходить через точку , лежить на поверхнi (1) i задаiться рiвнянням

де точцi Вавiдповiдаi параметр .

Оскiльки крива лежить на поверхнi, то координати ii точок задовольняють рiвняння (1):

. (2)

Диференцiюючи рiвнiсть (2), маiмо:

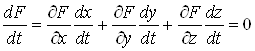. (3)

Ця рiвнiсть показуi, що вектори (рис. 1)

ортогональнi, причому другий з них i напрямним вектором дотичноi до кривоi Вау точцi .

Крiм того, з рiвностi (3) випливаi, що дотичнi до всiх кривих, якi проходять через точку Ваi лежать на поверхнi (1), ортогональнi до одного й того самого вектора . Тодi всi цi дотичнi лежать в однiй i тiй самiй площинi, яка називаiться дотичною площиною до поверхнi в точцi .

Знайдемо рiвняння дотичноi площини. Оскiльки ця площина проходить через точку Ваперпендикулярно до вектора , то ii рiвняння маi вигляд.

.(4)

Нормаллю до поверхнi в точцi Ваназивають пряму, що проходить через точку перпендикулярно до дотичноi площини в цiй точцi.

Оскiльки нормаль проходить через точку Ваi маi напрямний вектор , то канонiчнi рiвняння нормалi мають такий вигляд:

. (5)

Якщо рiвняння поверхнi задано в явнiй формi, то, поклавши, отримаiмо

,

тодi рiвняння (4) i (5) наберуть вигляду:

;(6)

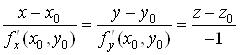.(7)

Рисунок 1 тАУ Дотична площина та нормаль до поверхнi

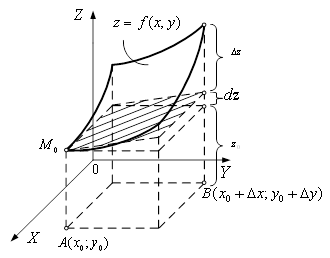
Рисунок 2 тАУ Геометричний змiст повного диференцiала функцii

З'ясуiмо геометричний змiст повного диференцiала функцii. Якщо у формулi (6) покласти, то ця формула запишеться у виглядi

.

Права частина цiii рiвностi i повним диференцiалом функцii Вав точцi, тому .

Таким чином, повний диференцiал функцii двох змiнних у точцi Вадорiвнюi приросту аплiкати точки на дотичнiй площинi до поверхнi в точцi, якщо вiд точки Ваперейти до точки Ва(рис. 2).

Зауваження 1.Ми розглянули випадок, коли функцiя Вадиференцiйована в точцi Ваi.

Якщо цi умови не виконуються в деякiй точцi (ii називають особливою), то дотична та нормаль в такiй точцi можуть не iснувати.

Зауваження 2.Якщо поверхня (1) i поверхнею рiвня для деякоi функцii, тобто, то вектор

буде напрямним вектором нормалi до цiii поверхнi рiвня.

2. Скалярне поле. Похiдна за напрямом. Градiiнт

Область простору, кожнiй точцi якоi поставлено у вiдповiднiсть значення деякоi скалярноi величини , називають скалярним полем.РЖнакше кажучи, скалярне поле тАУ це скалярна функцiя Варазом з областю ii визначення.

Рисунок 3.3 тАУ Вектор

Прикладами скалярних полiв i поле температури даного тiла, поле густини даного неоднорiдного середовища, поле вологостi повiтря, поле атмосферного тиску, поле потенцiалiв заданого електростатичного поля тощо.

Для того щоб задати скалярне поле, достатньо задати скалярну функцiю Ваточки Ваi область ii визначення.

Якщо функцiя Ване залежить вiд часу, то скалярне поле називають стацiонарним, а скалярне поле, яке змiнюiться з часом, тАУ нестацiонарним. Надалi розглядатимемо лише стацiонарнi поля.

Якщо в просторi ввести прямокутну систему координат,то точка Вав цiй системi матиме певнi координати Ваi скалярне поле u стане функцiiю цих координат:

.

Якщо скалярна функцiя Вазалежить тiльки вiд двох змiнних, наприклад x i , то вiдповiдне скалярне поле Ваназивають плоским;якщо ж функцiя Вазалежить вiд трьох змiнних: x, i, то скалярне поле Ваназивають просторовим.

Геометрично плоскi скалярнi поля зображують за допомогою лiнiй рiвня, а просторовi тАУ за допомогою поверхонь рiвня.

Для характеристики швидкостi змiни поля в заданому напрямi введемо поняття похiдноi за напрямом.

Нехай задано скалярне поле . Вiзьмемо в ньому точку Ваi проведемо з цiii точки вектор, напрямнi косинуси якого .

На векторi Вана вiдстанi Вавiд його початку вiзьмемо точку .

Тодi

.

Обчислимо тепер прирiст Вафункцii Вапри переходi вiд точки Вадо точки Вау напрямi вектора:

.

Якщо iснуi границя вiдношення Вапри, то цю границю називають похiдною функцii Вав точцi Ваза напрямом вектораi позначають,тобто

.

Виведемо формулу для обчислення похiдноi за напрямом. Припустимо, що функцiя Вадиференцiйована в точцi M.Тодi ii повний прирiст у цiй точцi можна записати так:

,

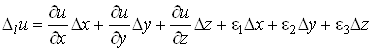де ВатАУ нескiнченно малi функцii при.

Оскiльки

то

.

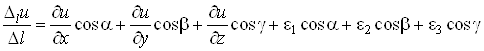Перейшовши до границi при, отримаiмо формулу для обчислення похiдноi за напрямом

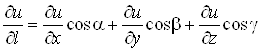.(8)

З формули (З.8) випливаi, що частиннi похiднi i окремими випадками похiдноi за напрямом. Дiйсно, якщо Вазбiгаiться з одним iз ортiв, Ваабо ,то похiдна за напрямом Вазбiгаiться з вiдповiдною частинною похiдною. Наприклад, якщо, то, тому

.

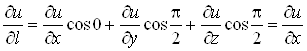Подiбно до того як частиннi похiднi Вахарактеризують швидкiсть змiни функцii в напрямi осей координат, так i похiдна Вапоказуi швидкiсть змiни скалярного поля Вав точцi Ваза напрямом вектора.

Абсолютна величина похiдноi Вавiдповiдаi значенню швидкостi, а знак похiдноi визначаi характер змiни функцii Вав напрямi Ва(зростання чи спадання).

Очевидно, що похiдна за напрямом, який протилежний напряму, дорiвнюi похiднiй за напрямом, взятiй з протилежним знаком.

Справдi, при змiнi напряму на протилежний кути Вазмiняться на , тому

.

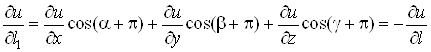Фiзичний змiст цього результату такий: змiна напряму на протилежний не впливаi на значення швидкостi змiни поля, а тiльки на характер змiни поля. Якщо, наприклад, в напрямi Ваполе зростаi, то в напрямi Вавоно спадаi, i навпаки.

Якщо поле плоске, тобто задаiться функцiiю Вато напрям вектора Вацiлком визначаiться кутом . Тому, поклавши у формулi (8) та, отримаiмо

.

Вектор, координатами якого i значення частинних похiдних функцii Вав точцi Ваназивають градiiнтом функцii в цiй точцi i позначають.Отже,

. (9)

Зв'язок мiж градiiнтом i похiдною в данiй точцi за довiльним напрямом показуi така теорема.

Теорема. Похiдна функцii Вау точцiза напрямом вектора Вадорiвнюi проекцii градiiнта функцii в цiй точцi на вектор, тобто

.(10)

Доведення

Нехай ВатАУ кут мiж градiiнтом (9) i одиничним вектором Ва(рис. 4), тодi з властивостей скалярного добутку [1] отримаiмо

Зазначимо деякi властивостi градiiнта.

1. Похiдна в данiй точцi за напрямом вектора Вамаi найбiльше

значення, якщо напрям вектора Вазбiгаiться з напрямом градiiнта, причому

.(11)

Справдi, з формули (10) випливаi, що похiдна за напрямом досягаi максимального значення (11), якщо , тобто якщо напрям вектора Вазбiгаiться з напрямом градiiнта.

Рисунок 4 тАУ Зв'язок мiж градiiнтом i похiдною за напрямом

Таким чином, швидкiсть зростання скалярного поля в довiльнiй точцi i максимальною у напрямi градiiнта.Зрозумiло, що у напрямi, протилежному до напряму градiiнта, поле найшвидше зменшуватиметься.

2. Похiдна за напрямом вектора, перпендикулярного до градiiнта, дорiвнюi нулю. РЖнакше кажучи, швидкiсть змiни поля у напрямi, перпендикулярному до градiiнта, дорiвнюi нулю, тобто скалярне поле залишаiться сталим.

Справдi, за формулою (10), якщо.

Вектор-градiiнт у кожнiй точцi поля Ваперпендикулярний до поверхнi рiвня, яка проходить через цю точку.Це твердження випливаi з того, що напрямний вектор нормалi до поверхнi рiвня, яка проходить через точку Вамаi координати (п. 1)

.

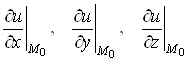4. Справедливi рiвностi:

.

Доведення

Доведемо, наприклад, третю рiвнiсть. Маiмо:

Решта рiвностей доводяться аналогiчно.

3. Формула Тейлора для функцii двох змiнних

Якщо функцiя однiii змiнноi Вамаi на вiдрiзку Ванеперервнi похiднi до -го порядку включно, то справджуiться формула Тейлора:

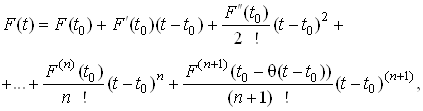(12)

.

Нехай ,

тодi, тому формулу (12) можна записати у виглядi

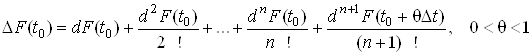.(13)

В аналогiчному виглядi формулу Тейлора можна отримати i для функцii багатьох змiнних. Розглянемо функцiю двох змiнних.

Нехай функцiя Вав областi Вамаi неперервнi частиннi похiднi до -го порядку включно. Вiзьмемо двi точки Вата Ватакi, щоб вiдрiзок Ваналежав областi.

Введемо нову змiнну :

, , .(14)

При Ваза цими формулами отримаiмо координати точки , а при ВатАУ координати точки . Якщо Вазмiнюватиметься на вiдрiзку , то точка опише весь вiдрiзок .Тодi вздовж цього вiдрiзка функцiя буде функцiiю однiii змiнноi :

.(15)

Запишемо формулу (13) для функцii (15) при:

.(16)

Обчислимо диференцiали, що входять у формулу (16). З рiвностей (14) i (15) маiмо

.

Оскiльки, то

.(17)

Аналогiчно

,

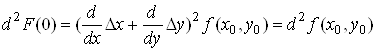.(18)

Продовжуючи цей процес, знайдемо

,

. (19)

Крiм того прирiст

.(20)

Пiдставивши вирази (17 тАУ 20) у формулу (14), отримаiмо

,(21)

.(22)

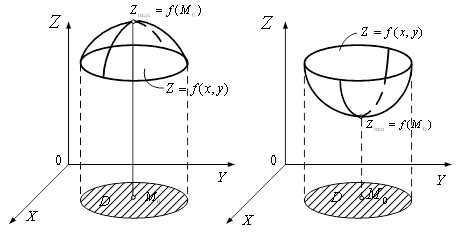
Рисунок 5 тАУ Локальний максимум (мiнiмум) функцii

Формулу (21) називають формулою Тейлора для функцii двох змiнних з залишковим членом Вау форму Лагранжа. Цю формулу використовують для наближених обчислень. Для рiзних значень з формули (21) можна отримати рiвностi для наближеного обчислення значень функцii. Абсолютну похибку цих наближених рiвностей оцiнюють через залишковий член (22).

Формула Тейлора (21) для функцii двох змiнних нагадуi формулу Тейлора (13) для функцii однiii змiнноi. Але насправдi, якщо розкрити вирази для диференцiалiв у формулi (21), то отримаiмо складнiшу формулу, нiж для

функцii однiii змiнноi. Наприклад, при Ваформула (21) маi вигляд:

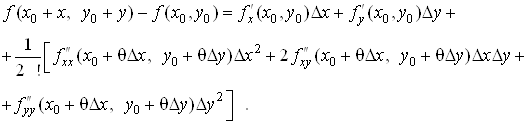(23)

4. Локальнi екстремуми функцii двох змiнних

Нехай функцiя Вавизначена в областi,а точка.Якщо iснуi окiл точки , який належить областi i для всiх вiдмiнних вiд Ваточок цього околу виконуiться нерiвнiсть,то точку Ваназивають точкою локального максимуму (мiнiмуму) функцii, а число ВатАУ локальним максимумом (мiнiмумом) цiii функцii (рис. 5). Точки максимуму та мiнiмуму функцii називають ii точками екстремуму.

Це означення можна перефразувати так. Покладемо , тодi

.

Якщо прирiст функцii Вапри всiх достатньо малих за абсолютною величиною приростах Ваi , то функцiя Вав точцi Вадосягаi локального максимуму Ва(локального мiнiмуму). РЖнакше кажучи, в околi екстремальноi точки прирости функцii мають один i той самий знак.

Теорема 1 (необхiднi умови екстремуму). Якщо функцiя маi в точцi Валокальний екстремум, то в цiй точцi частиннi похiднi першого порядку за змiнними x та Вадорiвнюють нулю або не iснують.

Доведення

Нехай ВатАУ точка екстремуму. Тодi функцiя Вабуде функцiiю однiii змiнноi. Ця функцiя маi екстремум у точцi ц, тому ii похiдна Вадорiвнюi нулю або не iснуi.

Аналогiчно, розглянувши функцiю Ваотримаiмо, що

дорiвнюi нулю або не iснуi.

Подiбна теорема справедлива для функцii змiнних. Точку, в якiй частиннi похiднi першого порядку функцii Вадорiвнюють нулю, тобто, називають стацiонарною точкою функцii.

Стацiонарнi точки та точки, в яких частиннi похiднi не iснують, називаються критичними точками.

Таким чином, якщо функцiя в будь-якiй точцi досягаi екстремуму, то це може статися лише в критичнiй точцi. Проте не всяка критична точка i точкою екстремуму, тобто теорема 1 встановлюi лише необхiднi, але не достатнi умови екстремуму. Наприклад, частиннi похiднi функцii Вадорiвнюють нулю в точцi. Але ця функцiя у вказанiй точцi екстремуму не маi, тому що в досить малому околi точки вона набуваi як додатних (при), так i вiд'iмних (при) значень.

Слiд зазначити, що в задачах з практичним змiстом, як правило, вiдомо, що функцiя маi екстремум. Якщо така функцiя маi лише одну критичну точку, то ця точка i буде точкою екстремуму.

Теорема 2 (достатнi умови екстремуму). Нехай у стацiонарнiй точцi Ваi деякому ii околi функцiя Вамаi неперервнi частиннi похiднi другого порядку. Якщо

,

то функцiямаi в точцi Ваекстремум, причому максимум при i мiнiмум при . Якщо , то в точцi Вафункцiя Ваекстремуму не маi.

Доведення

Запишемо формулу Тейлора (23) для функцii Вав околi стацiонарноi точки.Враховуючи, що, отримаiмо:

У випадку мiнiмуму для довiльних достатньо малих значень Вата Ваправа частина цiii рiвностi маi бути додатною, а у випадку максимуму тАУ вiд'iмною.

Внаслiдок неперервностi других частинних похiдних для цього достатньо, щоб диференцiал другого порядку в точцi

зберiгав знак для малих значень Вата.

Введемо такi позначення, , , тодi

.

Нехай ВатАУ кут мiж вiдрiзком , де ВатАУ точка з координатами Ваi вiссю; тодi., тому при Вамаiмо

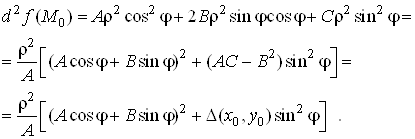
Розглянемо тепер птАЩять можливих випадкiв.

1. Нехай Ваi, тодi , тому при досить малих значеннях Ваприрiст, тобто функцiя Вамаi в точцi Вамаксимум.

2. Аналогiчно доводимо, що коли Ваi, то функцiя Вамаi в точцi Вамiнiмум.

Нехай Ваi. Якщо з точки Варухатися вздовж променя

, то. Якщо взяти Ватаким, щоб Ваабо , то

.

Отже, при малих значеннях Ваприрiст Вав околi точки Ване зберiгаi знак, тому ця точка не i точкою екстремуму функцii.

4. Аналогiчно встановлюiмо, що коли Ваi, то функцiя Вав точцi Ватакож не маi екстремуму.

5. Нехай Ваi, тодi Ваi

.

При досить малих кутах Вазнак величини Вазбiгаiться зi знаком , тому знак величини Вазалежатиме вiд знака множника. Але знак величини Вазмiнюiться при Ваi, бо . Отже, в достатньо малому околi точки Вазнак Ване збiгаiться, тобто функцiя Вав цiй точцi екстремуму не маi.

Зауваження. З доведення теореми 2 випливають так званi другi достатнi умови екстремуму: функцiя Вамаi мiнiмум у стацiонарнiй точцi, якщо диференцiал другого порядку в цiй точцi , i максимум тАУ якщо .

Можна довести, що другi достатнi умови екстремуму справедливi для функцiй довiльного числа змiнних.

На основi теорем 1 i 2 отримаiмо правило дослiдження диференцiйовних функцiй двох змiнних на екстремум. Щоб знайти екстремум диференцiйовноi функцii, необхiдно:

1) знайти стацiонарнi точки функцii iз системи рiвнянь:

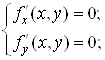
2) у кожнiй стацiонарнiй точцi Ваобчислити вираз

;

якщо , то ВатАУ точка екстремуму функцii, причому точка максимуму при Ваi мiнiмуму при; якщо, то точка Ване i точкою екстремуму функцii;

3) обчислити значення функцii Вау точках максимуму та мiнiмуму.

Якщо, то нiякого висновку про характер стацiонарноi точки зробити не можна i потрiбне додаткове дослiдження.

5. Найбiльше та найменше значення функцii

диференцiал функцiя дотична нормаль екстремум

Вiдомо, що функцiя, задана i неперервна в замкненiй та обмеженiй областi, досягаi в цiй областi найбiльшого i найменшого значень. У внутрiшнiх точках областi диференцiйовна функцiя може набувати цих значень лише в точках локального екстремуму. Тому потрiбно знайти всi стацiонарнi точки функцii, якi належать областi,розв'язавши систему рiвнянь, Ваi обчислити значення функцii в цих точках. Потiм потрiбно дослiдити функцiю на екстремум на межi областi.Використовуючи рiвняння межi, цю задачу зводять до знаходження абсолютного екстремуму функцii однiii змiнноi [8]. Серед здобутих таким чином значень функцii всерединi i на межi областi вибирають найбiльше i найменше значення.

Зазначимо, що загального методу знаходження найбiльшого та найменшого значень для довiльноi неперервноi функцii в замкненiй та обмеженiй областi Ванемаi.

Вместе с этим смотрят:

РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора

Актуальные проблемы квантовой механики

Алгебра и алгебраические системы

Анализ эмпирического распределения

Аналитическая теория чисел. L-функция Дирихле