Аппроксимация функции методом наименьших квадратов

АППРОКСИМАЦИЯ ФУНКЦИИ МЕТОДОМ НАИМЕНЬШИХ

КВАДРАТОВ

Содержание

1. Цель работы

2. Методические указания

2.1 Методические рекомендации по аппроксимации методом наименьших квадратов

2.2 Постановка задачи

2.3 Методика выбора аппроксимирующей функции

2.4 Общая методика решения

2.5 Методика решения нормальных уравнений

2.6 Рекомендации по выбору формы записи систем линейных алгебраических уравнений

2.7 Методика вычисления обратной матрицы

3. Ручной счет

3.1 Исходные данные

3.2 Система нормальных уравнений

3.3 Решение систем методом обратной матрицы

4. Схема алгоритмов

5. Текст программы

6. Результаты машинного расчета

Вывод

1. Цель работы

Настоящая курсовая работа является завершающим разделом дисциплины ВлВычислительная математика и программированиеВ» и требует от студента в процессе ее выполнения решения следующих задач:

а) практического освоения типовых вычислительных методов прикладной информатики; б) совершенствования навыков разработки алгоритмов и построения программ на языке высокого уровня.

Практическое выполнение курсовой работы предполагает решение типовых инженерных задач обработки данных с использованием методов матричной алгебры, решения систем линейных алгебраических уравнений численного интегрирования. Навыки, приобретаемые в процессе выполнения курсовой работы, являются основой для использования вычислительных методов прикладной математики и техники программирования в процессе изучения всех последующих дисциплин при выполнении курсовых и дипломных проектов.

2. Методические указания

2.1 Методические рекомендации по аппроксимации методом наименьших квадратов

2.2 Постановка задачи

При изучении зависимостей между величинами важной задачей является приближенное представление (аппроксимация ) этих зависимостей с помощью известных функций или их комбинаций, подобранных надлежащим образом. Подход к такой задаче и конкретный метод её решения определяются выбором используемого критерия качества приближения и формой представления исходных данных.

2.3 Методика выбора аппроксимирующей функции

Аппроксимирующую функцию 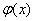выбирают из некоторого семейства функций, для которого задан вид функции, но остаются неопределенными (и подлежат определению) её параметры 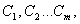т.е.

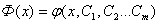
(1)

Определение аппроксимирующей функции φ разделяется на два основных этапа:

Подбор подходящего вида функции ;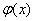

Нахождение ее параметров в соответствии с критерием МНК.

Подбор вида функции 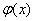Вапредставляет собой сложную задачу, решаемую методом проб и последовательных приближений. Исходные данные, представленные в графической форме (семейства точек или кривые), сопоставляется с семейством графиков ряда типовых функций, используемых обычно для целей аппроксимации. Некоторые типы функций 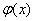, используемых в курсовой работе, приведены в таблице 1.

ВаБолее подробные сведения о поведении функций, которые могут быть использованы в задачах аппроксимации, можно найти в справочной литературе. В большинстве заданий курсовой работы вид аппроксимирующей функции 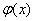задан.

2.4 Общая методика решения

После того как выбран вид аппроксимирующей функции 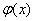Ва(или эта функция задана) и, следовательно, определена функциональная зависимость (1), необходимо найти в соответствии с требованиями МНК значения параметров С₁, С₂, тАж, С_m_. Как уже указывалось, параметры должны быть определены таком образом, чтобы значение критерия в каждой из рассматриваемых задач было наименьшим по сравнению с его значением при других возможных значениях параметров.

Для решения задачи подставим выражение (1) в соответствующее из выражений и проведем необходимые операции суммирования или интегрирования (в зависимости от вида I). В результате величина I, именуемая в дальнейшем критерием аппроксимации, представляется функцией искомых параметров

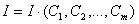
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(2)

Последующее сводиться к отысканию минимума этой функции переменных С_k; определение значений С_k=C_k^*, к=1,m, соответствующих этому элементу I, и является целью решаемой задачи.

Типы функций Таблица 1

Вид функции	Название функции
Y=C₁+C₂В·x	Линейная
Y=C₁+C₂В·x+C₃В·x²	Квадратичная (параболическая)
Y=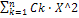	Рациональная(полином n^-й степени)
Y=C₁+C₂В·	Обратно пропорциональная
Y=C₁+C₂В·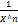	Степенная дробно-рациональная
Y=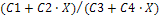	Дробно-рациональная(первой степени)
Y=C₁+C₂В·X^C3	Степенная
Y=C₁+C₂В·a^C3В·^x	Показательная
Y=C₁+C₂В·log_ax	Логарифмическая
Y=C₁+C₂В·Xⁿ (0	Иррациональная, алгебраическая
Y=C₁В·sinx+C₂cosx	Тригонометрические функции (и обратные к ним)

Возможны следующие два подхода к решению этой задачи: использование известных условий минимума функции нескольких переменных или непосредственное отыскание точки минимума функции каким тАУ либо из численных методов.

Для реализации первого из указанных подходов воспользуемся необходимым условием минимума функции (1) нескольких переменных, в соответствии с которыми в точке минимума должны быть равны нулю частные производные этой функции по всем ее аргументам

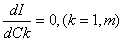
Полученные m равенств следует рассматривать как систему уравнений относительно искомых С₁, С₂,тАж, С_m. При произвольном виде функциональной зависимости (1) уравнения (3) оказывается нелинейным относительно величин C_k и их решение требует применение приближенных численных методов.

Использование равенства (3) дают, лишь необходимые, но недостаточные условия минимума (2). Поэтому требуется уточнить, обеспечивают ли найденные значения C_k^*именно минимум функции 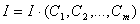. В общем случае такое уточнение выходит за рамки данной курсовой работы, и предлагаемые для курсовой работы задания подобраны так, что найденное решение системы (3) отвечает именно минимуму I. Однако, поскольку величина I неотрицательна (как сумма квадратов) и нижняя её граница есть 0 (I=0), то, если существует решение системы (3) единственно, оно отвечает именно минимуму I.

При представлении аппроксимирующей функции 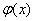Ваобщим выражением (1) соответствующие нормальным уравнениям (3) оказываются нелинейными относительно искомых С_к. их решение может быть сопряжено со значительными трудностями. В таких случаях предпочтительным являются непосредственный поиск минимума функции 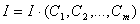в области возможных значений ее аргументов С_к , не связанный с использованием соотношений (3). Общая идея подобного поиска сводиться к изменению значений аргументов С_к и вычислению на каждом шаге соответствующего значения функции I до минимального или достаточно близко к нему.

2.5 Методика решения нормальных уравнений

Один из возможных способов минимизации критерия аппроксимации (2) предполагает решение системы нормальных уравнений (3). При выборе в качестве аппроксимирующей функции линейной функции искомых параметров нормальные уравнения представляют собой систему линейных алгебраических уравнений.

2.6 Рекомендации по выбору формы записи систем линейных алгебраических уравнений

Систему n линейных уравнений общего вида:

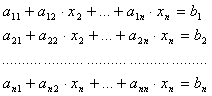
Ва(4)

(4) можно записать посредством матричных обозначений в следующем виде: АВ·Х=В,

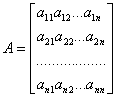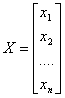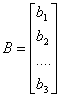; ; ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (5)

квадратная матрица А называется матрицей системы, а вектора Х и В соответственно вектором-столбцом неизвестных систем и вектором-столбцом ее свободных членов.

В матричном виде исходную систему n линейных уравнений можно записать и так:

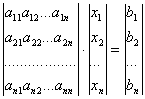
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(6)

Решение системы линейных уравнений сводиться к отысканию значений элементов вектора-столбца (х_i), называемых корнями системы. Чтобы эта система имела единственное решение, входящее в нее n уравнение должно быть линейно независимым. Необходимым и достаточным условием этого является неравенство нулю определителя системы, т.е. Δ=detA≠0.

Алгоритм решения системы линейных уравнений подразделяется на прямые и итерационные. На практике никакой метод не может быть бесконечным. Для получения точного решения итерационные методы требуют бесконечного числа арифметических операций. практически это число приходиться брать конечным и поэтому решение в принципе имеет некоторую ошибку, даже если пренебречь ошибками округлений, сопровождающими большинство вычислений. Что же касается прямых методов, то они даже при конечном числе операций могут в принципе дать точное решение, если оно существует.

Прямые и конечные методы позволяют найти решение системы уравнений за конечное число шагов. Это решение будет точным, если все промежутки вычисления проводятся с ограниченной точностью.

2.7 Методика вычисления обратной матрицы

Один из методов решения системы линейных уравнений (4), записываем в матричной форме АВ·Х=В, связан с использованием обратной матрицы А^-1. В этом случае решение системы уравнений получается в виде

Х=А^-1В·В,

где А^-1тАУматрица, определяемая следующим образом.

Пусть А тАУквадратная матрица размером n х n с ненулевым определителем detA≠0. Тогда существует обратная матрица R=A^-1, определяемая условием AВ·R=E,

где Е тАУединичная матрица, все элементы главной диагонали которой равны I, а элементы вне этой диагонали -0, Е=[E₁,.., E_n], где Е_i тАУвектор-столбец. Матрица К тАУквадратная матрица размером n х n.

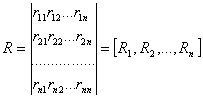
где Rj тАУвектор-столбец.

Рассмотрим ее первый столбец R=( r₁₁, r₂₁,тАж, r_n₁)^T, где Т тАУозначает транспонирование. Нетрудно проверить, что произведение AВ·R равно первому столбцу E₁=(1, 0, тАж, 0)^Т единичной матрицы Е, т.е. вектор R₁ можно рассмотреть как решение системы линейных уравнений AВ·R₁=E_1.Аналогично m тАУй столбец матрицы R , Rm, 1≤ m ≤ n, представляет собой решение уравнения AВ·Rm=Em, где Em=(0, тАж, 1, 0)^T m тАУй столбец единичной матрицы Е.

Таким образом, обратная матрица R представляет собой набор из решений n систем линейных уравнений

AВ·Rm=Em , 1≤ m ≤ n.

Для решения этих систем можно применять любые методы, разработанные для решения алгебраических уравнений. Однако метод Гаусса дает возможность решать все эти n систем одновременно, а независимо друг от друга. Действительно, все эти системы уравнений отличаются только правой частью, а все преобразования, которые проводятся в процессе прямого хода метода Гаусса, полностью определяются элементами матрицы коэффициентов (матрицы А). Следовательно, в схемах алгоритмов изменению подлежат только блоки, связанные с преобразованием вектора В. В нашем случае одновременно будут преобразовываться n векторов Em, 1≤ m ≤ n. Результатом решения также будет не один вектор, а n векторов Rm, 1≤ m ≤ n.

3. Ручной счет

3.1 Исходные данные

Xi	0,3	0,5	0,7	0,9	1,1
Yi	1,2	0,7	0,3	-0,3	-1,4

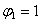
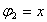
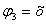
Метод MINU

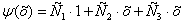
3.2 Система нормальных уравнений

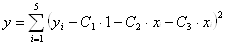
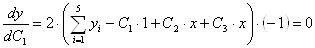
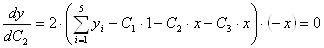
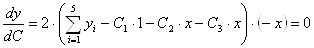
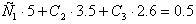
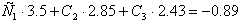
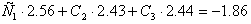
3.3 Решение систем методом обратной матрицы

аппроксимация квадрат функция линейный уравнение

5 3,5 2,6 0,5 5 3,5 2,6 0,5

3,5 2,85 2,43 -0,89ВаВаВаВаВаВаВаВа 0 0,4Ва 0,61 -1,24

2,56 2,43 2,44 -1,86 0 0,638ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа 1,109 -2,116

5 3,5 2,6 0,5ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа

0 0,4 0,61 -1,24

0 0 0,136 -0,138

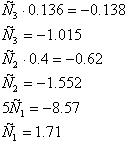
Результаты расчета:

С₁=1,71; С₂=-1,552; С₃=-1,015;

Аппроксимирующая функция:

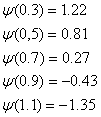
4. Текст программы

Program ApprF;

Uses Crt;

const n=3;

type

Ваmass=array[1.5]of real;

Ваmass1=array[1.3,1.3] of real;

Ваmass2=array[1.3] of real;

var

ВаX,Y,E,y1,delta : mass;

ВаA: mass1;

ВаB,x1: mass2;

Ваbig,r,sum,temp,maxD,Q:real;

Ваi,j,k,l,num : byte;

Procedure VVOD(var E: mass);

Begin

ВаFor i:=1 to 5 do

Ваread(E[i]);

Ваwriteln;

End;

Function FI( i ,k : integer): real;

ВаBegin

Ваif i=1 then FI:=1;

Ваif i=2 then FI:=Sin(x[k]);

Ваif i=3 then FI:=Cos(x[k]);

End;

ВаProcedure PEREST(i:integer;var a:mass1;var b:mass2);

Ваbegin

Ваbig:=0;

Ваnum:=0;

Ваfor l:= i to 3 do

Ваif abs(a[l,i]) > big then

Ваbegin

Ваbig:=a[l,i]; writeln ( big:6:4);

Ваnum:=l;

Ваend;

Ваif big=0 then

Ваwriteln('Перестановка уравнений');

Ваif num<>i then

Ваfor j:=i to 3 do

Ваbegin

Ваtemp:=a[i,j];

Ваa[i,j]:=a[num,j];

Ваa[num,j]:=temp;

Ваend;

Ваtemp:=b[i];

Ваb[i]:=b[num];

Ваb[num]:=temp;

Ваend;

ВаBegin

Ваwriteln('__________________');

Ваwriteln('Введите значения Х');

ВаVVOD(X) ;

Ваwriteln('__________________');

Ваwriteln('тАЪВведите значения Y');

ВаVVOD(Y);

Ваwriteln('___________________');

ВаFor i:=1 to 3 do

ВаFor j:=1 to 3 do

Ваbegin

ВаA[i,j]:=0;

ВаFor k:=1 to 5 do

Ваbegin A[i,j]:= A[i,j]+FI(i,k)*FI(j,k); write(a[i,j]:7:5); end;

Ваend;

Ваwriteln('________________________');

writeln('Матрица Коэффициентов Ai,j');

writeln('__________________________');

ВаFor i:=1 to 3 do

Ваbegin

ВаFor j:=1 to 3 do

Ваwrite (A[i,j]:5:2, ' ');

Ваwriteln;

Ваend;

ВаFor i:=1 to 3 do

Ваbegin

ВаB[i]:=0;

ВаFor j:=1 to 5 do

ВаB[i]:=B[i]+Y[j]*FI(i,j);

Ваend;

Ваwriteln;

Ваreadkey;

writeln('__________________________');

writeln(тАШМатрица Коэффициентов Bi ');

writeln('_________________________');

ВаFor i:=1 to 3 do

Ваwrite(B[i]:5:2, ' ');

Ваwriteln;

Ваfor i:=1 to 2 do

Ваbegin

ВаPEREST(i,a,b);

Ваfor k:=i+1 to 3 do

Ваbegin

ВаQ:=a[k,i]/a[i,i]; writeln('g=',Q);

Ваa[k,i]:=0;

Ваfor j:=i+1 to 3 do

Ваa[k,j]:=a[k,j]-Q*a[i,j]; writeln('a=',a[k,j]);

Ваb[k]:=b[k]-Q*b[i]; writeln('b=',b[k]);

Ваend;

Ваx1[n]:=b[n]/a[n,n];

Ваwrite(x1[n]);

Ваfor i:=2 downto 1 do

Ваbegin

Ваsum:=b[i];

Ваfor j:=i+1 to 3 do

Ваsum:=sum-a[i,j]*x1[j];

Ваx1[i]:=sum/a[i,i];

end;

Ваwriteln('__________________________');

Ваwriteln ('Значение коэффициентов ');

Ваwriteln('_________________________');

Ваfor i:=1 to 3 do

Ваwriteln( ' C',i,'=',x1[i]);

Ваk:=1;

Ваfor i:=1 to 5 do

Ваbegin

Ваy1[i]:= x1[k]*FI(k,i) + x1[k+1]*FI(k+1,i) + x1[k+2]*FI(k+2,i);

Ваdelta[i]:=abs (y[i]-y1[i]);

Ваwriteln;

Ваwriteln (y1[i]);

Ваend;

Ваfor i:=1 to 3 do

Ваwrite (x1[i]:7:3);

Ваwriteln;

ВаmaxD:=delta[1];

Ваfor i:=1 to 5 do

Ваif delta[i]>maxD then maxD:=delta[1];

Ваwriteln ('max Delta= ', maxD:5:3);

ВаEnd.

5. Результаты машинного расчета

С₁=1,511; С₂=-1,237; С₃=-1,11;

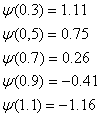
Вывод

В процессе выполнения курсовой работы я практически освоил типовые вычислительные методы прикладной математики, совершенствовал навыки разработки алгоритмов и построения программ на языках высокого уровня. Получил навыки, являющиеся основой для использования вычислительных методов прикладной математики и техники программирования в процессе изучения всех последующих дисциплин при выполнении курсовых и дипломных проектов.

Вместе с этим смотрят:

РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора

Актуальные проблемы квантовой механики

Алгебра и алгебраические системы

Анализ эмпирического распределения

Аналитическая теория чисел. L-функция Дирихле