Дифференциальная геометрия поверхностей Каталана
Содержание
Глава 1.Введение в дифференциальную геометрию поверхностей. Основные понятия
1.1 Первая квадратичная форма поверхности
1.2 Внутренняя геометрия поверхности
1.3 Вторая квадратичная форма поверхности
1.4 Классификация точек регулярной поверхности
1.5 Средняя и гауссова кривизны поверхности
Глава 2. Понятие поверхности Каталана
2.1 Общие положения
2.2 Примеры поверхностей Каталана
2.3 Виды поверхностей Каталана
Глава 3. Дифференциальная геометрия поверхностей Каталана
3.1 Первая и вторая квадратичные формы линейчатой поверхности
3.2 Первая и вторая квадратичные формы поверхности Каталана
3.3 О коноидах
Глава 4. Специальные поверхности Каталана (поверхности класса КА)
4.1 Вывод уравнения поверхности класса КА
4.2 Вывод уравнения поверхности класса КА по заданным кривым и нормальному вектору порождающей плоскости
Глава 5. Дифференциальная геометрия поверхностей класса КА
5.1 Первая и вторая квадратичные формы линейчатой поверхности
5.2 Первая квадратичная форма поверхности класса КА
5.3 Вторая квадратичная форма поверхности класса КА
Глава 6. О программе визуализации и анализа поверхностей
6.1 Общие положения и возможности программы
6.2 Примеры работы
Выводы
Список литературы
Глава 1. Введение в дифференциальную геометрию поверхностей.
Основные понятия
1.1 Первая квадратичная форма поверхности
Пусть 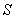 Ва- гладкая поверхность,
Ва- гладкая поверхность, 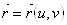 ВатАУ ее векторное параметрическое уравнение и
ВатАУ ее векторное параметрическое уравнение и 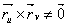 .
.
Определение 1.1.
Первой квадратичной формой на поверхности 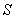 Ваназывается выражение
Ваназывается выражение
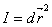 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1)
Распишем это выражение подробнее.
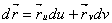 ,
,
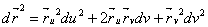
Откуда 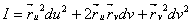 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа(2)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа(2)
Выражение (2) в каждой точке поверхности 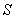 Вапредставляет собой квадратичную форму от дифференциалов
Вапредставляет собой квадратичную форму от дифференциалов 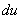 Ваи
Ваи 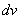 . Первая квадратичная форма является знакоположительной, так как ее дискриминант
. Первая квадратичная форма является знакоположительной, так как ее дискриминант
 Ваи
Ваи 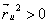 .
.
Для коэффициентов первой квадратичной формы часто используют следующие обозначения (и мы в своих исследованиях будем придерживаться именно их) ([1].[2],[3]):
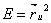 ,
,
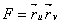 ,
,
 .
.
Так что выражение (2) для формы 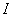 Ваможно переписать в виде
Ваможно переписать в виде
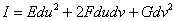 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3)
Соответственно,
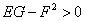 .
.
1.2 Внутренняя геометрия поверхности
Известно, что, зная первую квадратичную форму поверхности, можно вычислять длины дуг кривых на поверхности, углы между кривыми и площади областей на поверхности. В самом деле, если рассмотреть формулы, определяющие вышеуказанные величины, можно заметить, что туда входят только лишь коэффициенты 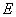 ,
, 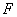 ,
,  Вапервой квадратичной формы. Поэтому если известная первая квадратичная форма поверхности, можно исследовать геометрию на поверхности, не обращаясь к ее уравнениям, а лишь используя ее первую квадратичную форму.
Вапервой квадратичной формы. Поэтому если известная первая квадратичная форма поверхности, можно исследовать геометрию на поверхности, не обращаясь к ее уравнениям, а лишь используя ее первую квадратичную форму.
Совокупность геометрических фактов, относящихся к поверхности, которые можно получить при помощи ее первой квадратичной формы, составляет так называемую внутреннюю геометрию поверхности.
Поверхности, имеющие одинаковые первые квадратичные формы и потому имеющие одинаковую внутреннюю геометрию, называются изометричными.
Рассмотрим простой пример.
Пусть задана поверхность
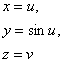
Это цилиндрическая поверхность с синусоидой в качестве направляющей.

Имеем:
 ,
, 
Поэтому
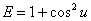 ,
,
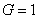 ,
,
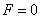
Следовательно,
 .
.
Если сделать замену, вводя новые параметры 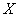 Ваи
Ваи  Ватаким образом
Ватаким образом
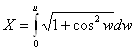 ,
,
 .
.
Тогда первая квадратичная форма поверхности примет, очевидно, вид
 .
.
Мы видим, что в новых переменных первая квадратичная форма рассматриваемой цилиндрической поверхности совпадает с первой квадратичной формой плоскости 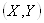 Ваи поэтому внутренняя геометрия этой поверхности совпадает с внутренней геометрией плоскости. Т.е. синусоидальный цилиндр изометричен плоскости. Этот важный факт мы еще получим несколько другим способом.
Ваи поэтому внутренняя геометрия этой поверхности совпадает с внутренней геометрией плоскости. Т.е. синусоидальный цилиндр изометричен плоскости. Этот важный факт мы еще получим несколько другим способом.
Чисто геометрически это свойство понятно: синусоидальный цилиндр получается изгибанием (т.е. деформацией без сжатий и растяжений) обычной плоскости. При такой деформации внутренняя геометрия не изменяется.
Более того, можно показать, что если одна поверхность получается из другой путем изгибания, то внутренние геометрии этих поверхностей совпадают.
1.3 Вторая квадратичная форма поверхности
1.3.1. Определение второй квадратичной формы.
Основным объектом рассмотрения в этой части изложения станет 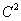 Ва- регулярная поверхность
Ва- регулярная поверхность 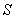 , заданная своим радиус-вектором.
, заданная своим радиус-вектором.
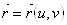 ,
, 
В каждой точке такой поверхности помимо единичного вектора нормали
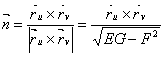 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1)
Определен и второй дифференциал радиус вектора
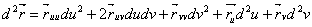 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2)
Определение 1.2.
Второй квадратичной формой поверхности 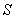 Ваназывается скалярное произведение векторов
Ваназывается скалярное произведение векторов 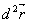 Ваи
Ваи 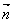 .
.
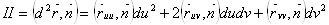 Ва([1],[3],[4],[5]) ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа(3)
Ва([1],[3],[4],[5]) ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа(3)
Нетрудно заметить, что в каждой точке поверхности  Ваквадратичная форма (3) является квадратичной формой относительно дифференциалов
Ваквадратичная форма (3) является квадратичной формой относительно дифференциалов 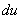 Ваи
Ваи 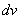 .
.
Для коэффициентов второй квадратичной формы приняты (и мы также в дальнейшем будем пользоваться этим) следующие обозначения
 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (4)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (4)
Это позволяет записать ее в следующем простом виде
 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (5)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (5)
Покажем еще один способ вычисления коэффициентов второй квадратичной формы поверхности.
Заменим в формулах (4) единичный вектор нормали 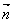 Вана его выражение (1), получим,
Вана его выражение (1), получим,
 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (6)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (6)
Для подробного вывода нужно знать тождество:
 .
.
Продолжим рассуждения.
Так как векторы 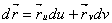 Ваи
Ваи 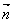 Ваортогональны (первый, разумеется лежит в касательной плоскости к поверхности, а второй лежит в плоскости нормального сечения).
Ваортогональны (первый, разумеется лежит в касательной плоскости к поверхности, а второй лежит в плоскости нормального сечения).
Поэтому
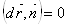 .
.
Откуда
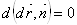
Отсюда, дифференцируя, получим:
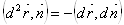 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (7)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (7)
Это дает еще один способ расчета второй квадратичной формы.
 ([5],[6])ВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(8)
([5],[6])ВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(8)
Отсюда же можно получить новые формулы для вычисления коэффициентов второй квадратичной формы. Впрочем, удобнее продифференцировать по 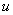 Ваи по
Ваи по  Ваочевидные равенства
Ваочевидные равенства
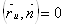 Ваи
Ваи 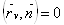 .
.
Воспользовавшись соотношениями (4), получаем, что
 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (9)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (9)
Вторая квадратичная форма эффективна при выяснении графических свойств регулярной поверхности.
1.4 Классификация точек регулярной поверхности
Пусть 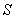 ВатАУ регулярная поверхность и
ВатАУ регулярная поверхность и 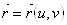 ВатАУ ее параметрическое задание.
ВатАУ ее параметрическое задание.
Выберем на поверхности 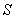 Ванекоторую точку
Ванекоторую точку 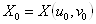 Ваи рассмотрим плоскость
Ваи рассмотрим плоскость 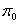 , которая касается поверхности
, которая касается поверхности 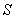 Вав этой точке.
Вав этой точке.
Отклонение произвольной точки 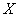 Ваповерхности
Ваповерхности 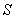 Ваот плоскости
Ваот плоскости 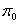 Ваопределим по формуле
Ваопределим по формуле
 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1)
В этой формуле  ВатАУ единичный вектор нормали к поверхности в точке
ВатАУ единичный вектор нормали к поверхности в точке 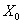 . Это отклонение, взятое по абсолютной величине, равно расстоянию от точки
. Это отклонение, взятое по абсолютной величине, равно расстоянию от точки 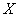 Вадо плоскости
Вадо плоскости 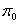 . Отклонение положительно, если точка
. Отклонение положительно, если точка 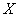 Ваи конец вектора
Ваи конец вектора  Валежат по одну сторону от касательной плоскости, соответственно, оно отрицательно, если они лежат по разные стороны от касательной плоскости в точке
Валежат по одну сторону от касательной плоскости, соответственно, оно отрицательно, если они лежат по разные стороны от касательной плоскости в точке 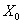 .
.
Рассмотрим формулу (1).
Разность  Вадопускает следующую интерпретацию
Вадопускает следующую интерпретацию
 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2)
Где
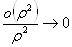 , при
, при  .
.
Умножим обе части равенства (2) скалярно на вектор  Ваи положив
Ваи положив
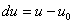 ,
, 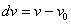 .
.
Получим, что
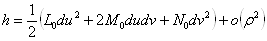 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3)
Разумеется, вдумчивый (или хотя бы немного читающий эти выкладки) читатель поймет, что коэффициенты
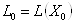 ,
,
 ,
,
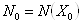
указанные в формуле (3) вычислены в точке 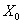 , в окрестности которой мы и рассматриваем исходную поверхность
, в окрестности которой мы и рассматриваем исходную поверхность 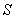 .
.
Из курса линейной алгебры известно, что свойства квадратичной формы во многом определяются ее дискриминантом. А скорее даже знаком квадратичной формы.
Вычислим дискриминант второй квадратичной формы в точке 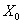 .
.

Рассмотрим все возможные случаи.([7],[8],[9],[10],[11])
Случай 1.
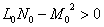
Т.е. вторая квадратичная форма поверхности в заданной точке является знакоопределенной.
Зафиксируем в точке 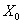 Ванекоторое направление на поверхности. Пускай
Ванекоторое направление на поверхности. Пускай 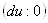 .
.
Тогда любое другое направление на поверхности в точке 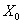 Ваможно задавать при помощи угла
Ваможно задавать при помощи угла 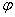 , который оно образует с уже выбранным направлением.
, который оно образует с уже выбранным направлением.
Положим
 ,
, 
Тогда
 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (4)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (4)
Нетрудно показать, что
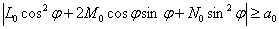 ,
,
где постоянная

а в силу условия
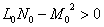 Ваположительна.
Ваположительна.
Таким образом неравенство
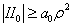
выполняется независимо от выбора угла 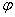 .
.
Так как порядок стремления к нулю при  Вавторого слагаемого
Вавторого слагаемого 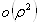 Вав правой части формулы (3) выше двух, то из последней оценки можно сделать следующий вывод.
Вав правой части формулы (3) выше двух, то из последней оценки можно сделать следующий вывод.
Отклонение 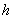 Васохраняет знак (совпадающий со знаком второй квадратичной формы
Васохраняет знак (совпадающий со знаком второй квадратичной формы 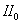 ) для всех достаточно малых значений
) для всех достаточно малых значений 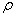 независимо от выбора направления на поверхности.
независимо от выбора направления на поверхности.
Это означает, что все точки поверхности 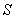 , достаточно близкие к точке
, достаточно близкие к точке 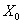 , располагаются по одну сторону от касательной плоскости поверхности
, располагаются по одну сторону от касательной плоскости поверхности 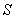 в этой точке. Такая точка поверхности называется эллиптической точкой.
в этой точке. Такая точка поверхности называется эллиптической точкой.
Например, все точки сфер тАУ эллиптические.([6],[8])

Случай 2.
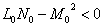 .
.
Вторая квадратичная форма является знакопеременной.
Покажем, что в этом случае, в точке 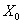 Ваможно указать два неколлинеарных направления на поверхности, обладающие следующими свойствами:
Ваможно указать два неколлинеарных направления на поверхности, обладающие следующими свойствами:
- для значений дифференциалов, определяющих эти направления, вторая квадратичная форма поверхности, вычисленная в точке 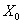 , обращается в нуль,
, обращается в нуль,
- все остальные направления на поверхности в точке 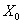 Варазбиваются на два класса тАУ для дифференциалов, определяющих направления одного из этих классов, вторая квадратичная форма положительна и для другого отрицательна.
Варазбиваются на два класса тАУ для дифференциалов, определяющих направления одного из этих классов, вторая квадратичная форма положительна и для другого отрицательна.
Пусть некоторое направление  Ваположительного класса задается углом
Ваположительного класса задается углом 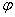 . В соответствии с формулой (4) имеем
. В соответствии с формулой (4) имеем
 , ([1],[4],[11])
, ([1],[4],[11])
где 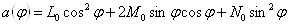
Как видно из формулы (3), знак отклонения 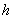 Вадля всех достаточно малых значений
Вадля всех достаточно малых значений 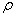 Вав рассматриваемом направлении
Вав рассматриваемом направлении 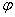 Васовпадает со знаком второй квадратичной формы
Васовпадает со знаком второй квадратичной формы 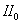 . Следовательно, если точка
. Следовательно, если точка 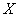 Ваповерхности
Ваповерхности 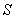 Вадостаточно близка к точке
Вадостаточно близка к точке 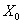 , то это отклонение положительно.
, то это отклонение положительно.
Рассуждая аналогично, можно указать точки на поверхности, близкие к точке 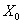 , для которых отклонение
, для которых отклонение 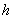 Вабудет отрицательным.
Вабудет отрицательным.
Приведенные рассуждения показывают, что вблизи точки 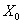 Ваповерхность
Ваповерхность 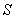 Варасполагается по разные стороны от касательной плоскости. При этом проекции точек поверхности, отклонения которых расположены на касательный плоскости заполняются множество ВлмеждуВ» этими направлениямитАж
Варасполагается по разные стороны от касательной плоскости. При этом проекции точек поверхности, отклонения которых расположены на касательный плоскости заполняются множество ВлмеждуВ» этими направлениямитАж
В этом случае точка называется гиперболической точкой поверхности.
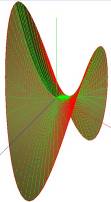
Случай 3.
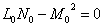 .
.
Но отличен от нуля хотя бы один из коэффициентов,  ,
, 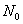 .
.
Пусть для определенности 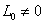 . Тогда вторая квадратичная форма поверхности
. Тогда вторая квадратичная форма поверхности 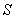 Вав точке
Вав точке 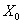 Ваможет быть записана в следующем виде
Ваможет быть записана в следующем виде
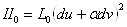
Тем самым в зависимости от знака 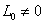 Ваформа
Ваформа 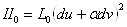 Валибо неотрицательна, либо неположительна. При этом на поверхности
Валибо неотрицательна, либо неположительна. При этом на поверхности 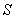 Вав точке
Вав точке 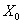 Ваможно указать направление
Ваможно указать направление 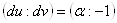 , такое, что определяющие его дифференциалы
, такое, что определяющие его дифференциалы 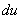 Ваи
Ваи 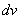 Ваобращают вторую квадратичную форму
Ваобращают вторую квадратичную форму 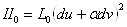 Вав нуль.
Вав нуль.
Для всех других направлений на поверхности в точке 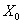 Ваформа имеет один и тот же знак (совпадающий со знаком
Ваформа имеет один и тот же знак (совпадающий со знаком  )
)
В этом случае точка 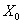 Ваназывается параболической точкой поверхности
Ваназывается параболической точкой поверхности 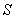 .
.
Случай 4. ([1],[11],[12])
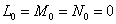
Такая точка 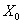 Ваназывается точкой уплощения поверхности. Расположение поверхности, близ таких точек может быть самым разнообразным.
Ваназывается точкой уплощения поверхности. Расположение поверхности, близ таких точек может быть самым разнообразным.
Например, все точки плоскости являются точками уплощения.
1.5 Средняя и гауссова кривизны поверхности
Нам осталось рассмотреть еще немного понятий, прежде чем приступить к исследованиям. Рассмотрим на поверхности 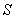 Вапроизвольную
Вапроизвольную 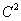 Ва- регулярную кривую, проходящую через точку
Ва- регулярную кривую, проходящую через точку 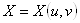 Вав направлении
Вав направлении  .
.
Пусть

- естественная параметризация кривой. Вычислим в точке 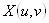 Ватри вектора
Ватри вектора
- единичный вектор касательной к кривой
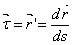 ,
,
- единичный вектор нормали к поверхности
- и вектор
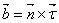
Эта тройка векторов линейно независима. Это позволяет представить вектор
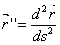
в виде линейной комбинации
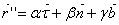
Так как 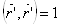 , то
, то
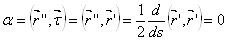 .
.
Коэффициенты 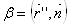 Ваи
Ваи  Ваимеют специальные названия.
Ваимеют специальные названия.
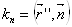 ВатАУ нормальная кривизна кривой
ВатАУ нормальная кривизна кривой
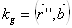 ВатАУ геодезическая кривизна кривой.
ВатАУ геодезическая кривизна кривой.
Примем без доказательства следующую формулу для вычисления нормальной кривизны поверхности в заданном направлении
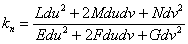 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1)
Как видно из этой формулы нормальная кривизна поверхности в данной точке зависит от направления на поверхности.
Определение 1.3.
Направление на поверхности называется главным, если нормальная кривизна в этом направлении достигает экстремального значения.
Покажем, что в каждой точке  -регулярной поверхности найдется не мене двух различных главных направлений.
-регулярной поверхности найдется не мене двух различных главных направлений.
Пусть  ВатАУ произвольное направление в точке
ВатАУ произвольное направление в точке 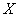 Вана поверхности
Вана поверхности 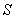 . Тогда
. Тогда
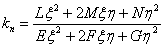 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(2)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(2)
(2) тАУ дифференцируемая функция переменных 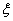 Ваи
Ваи 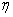 . Отметим, что функции коэффициентов второй и первой квадратичных форм определяются только выбором точки
. Отметим, что функции коэффициентов второй и первой квадратичных форм определяются только выбором точки 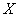 Ваи от переменных
Ваи от переменных 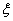 Ваи
Ваи 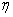 Ване зависят.
Ване зависят.
Полагая
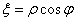 ,
,
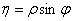
получим, что
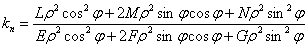
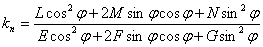
Так как функция
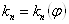 Ванепрерывна и
Ванепрерывна и  , то на отрезке
, то на отрезке 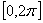 Ваона либо постоянна, либо имеет хотя бы один максимум. Это и означает, что в каждой точке
Ваона либо постоянна, либо имеет хотя бы один максимум. Это и означает, что в каждой точке 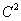 Ва- регулярной поверхности есть два различных главных направления.
Ва- регулярной поверхности есть два различных главных направления.
Определение 1.4.
Экстремальные значения нормальных кривизн в главных направлениях называются главными кривизнами поверхности в данной точке.
Укажем способ вычисления главных кривизн в данной точке регулярной поверхности.
Из формулы (2) вытекает тождество относительно переменных 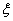 Ваи
Ваи 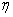
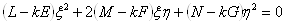 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3)
Продифференцируем это тождество по 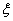 . Учитывая, что производная нормальной кривизны в главном направлении обращается в нуль, получим для главного направления
. Учитывая, что производная нормальной кривизны в главном направлении обращается в нуль, получим для главного направления 
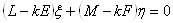 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (4)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (4)
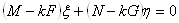 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(5)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(5)
Здесь 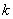 ВатАУ главная кривизна в направлении
ВатАУ главная кривизна в направлении  .
.
Рассматривая полученные соотношения (4) и (5) как систему линейных алгебраических уравнений относительно неизвестных 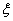 Ваи
Ваи 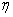 , получим, что эта система всегда имеет ненулевое решение, так как в данной точке регулярной поверхности всегда есть главные направления.
, получим, что эта система всегда имеет ненулевое решение, так как в данной точке регулярной поверхности всегда есть главные направления.
Из этого вытекает, что
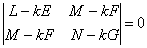
Вычисляя определитель, мы получим квадратное уравнение для искомой функции 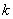 Ва(вниманиетАж мы его будем использовать при некоторых выкладках далее).
Ва(вниманиетАж мы его будем использовать при некоторых выкладках далее).
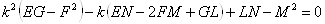 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (6)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (6)
Возможны два случая.
Случай 1.
Квадратное уравнение имеет два различных корня 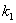 Ваи
Ваи 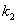 .
.
Этим корням на поверхности соответствует два различных главных направления.
Случай 2.
Уравнение (6) имеет один корень кратности 2 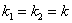 .
.
Это могут быть только точки уплощения 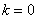 Ваили омбилические точки (точки округления) (
Ваили омбилические точки (точки округления) (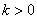 ).
).
Определение 1.5.
Средней кривизной 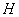 Ваповерхности в данной точке называется полусумма ее главных кривизн в этой точке.
Ваповерхности в данной точке называется полусумма ее главных кривизн в этой точке.
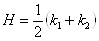 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (7)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (7)
Определение 1.6.
Гауссовой кривизной 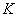 Ваповерхности называется произведение ее главных кривизн.
Ваповерхности называется произведение ее главных кривизн.
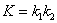 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (8)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (8)
В виду уравнения (6) можно показать, что
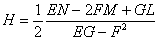 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (9)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (9)
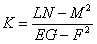 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа(10)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа(10)
Этих основных понятий нам пока хватит для рассмотрения специального класса поверхностей.
Глава 2. Понятие поверхности Каталана
2.1 Общие положения
Определение 2.1.
Поверхность Каталана тАУ линейчатая поверхность, прямолинейные образующие которой параллельны одной и той же плоскости.
Определение 2.2.
Плоскость, которой параллельны образующие поверхности Каталана, называется плоскостью параллелизма.
Определение 2.3.
Поверхность Каталана, все образующие которой пересекают одну прямую, называется Коноидом.
Замечание 2.1.
Обычно предполагают, что уравнение поверхность Каталана:
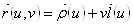 , причем
, причем  .
.
Мы, однако, не будем учитывать это условие, а ограничимся указанным выше определением. И те, и другие поверхности мы будем для краткости называть поверхностями Каталана.
Замечание 2.2.
Из определения поверхности Каталана следует, что, если ее уравнение:
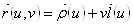 , то
, то 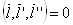 .
.
Это очевидно, так как все три вектора (вычисленные при одном и том же значении параметра), участвующие в смешанном произведении лежат в одной плоскости, тАУ плоскости параллелизма, т.е. они компланарны.
Для обратного утверждения справедлива теорема.
Теорема 2.1.
Достаточное условие того, что данная линейчатая поверхность является поверхностью Каталана.
Пусть задана линейчатая поверхность
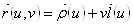 ,
,
причем вектор-функция 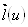 Ватрижды непрерывно дифференцируема (здесь и далее мы говорим о каком-либо простом куске поверхности, которому отвечают некоторые промежутки параметров). Тогда если
Ватрижды непрерывно дифференцируема (здесь и далее мы говорим о каком-либо простом куске поверхности, которому отвечают некоторые промежутки параметров). Тогда если  и
и 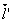 Ванеколлинеарен
Ванеколлинеарен  Вани в одной точке то данная поверхность является поверхностью Каталана.
Вани в одной точке то данная поверхность является поверхностью Каталана.
Доказательство.
Рассмотрим два случая: когда кривая, описываемая вектором 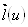 ВатАУ плоская и когда она неплоская.
ВатАУ плоская и когда она неплоская.
1) Предположим, что кривая 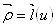 ВатАУ плоская. Тогда равенство
ВатАУ плоская. Тогда равенство 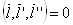 Вапросто следует из этого факта. Очевидно, что все тройки векторов (при любом значении параметра) лежат в плоскости кривой
Вапросто следует из этого факта. Очевидно, что все тройки векторов (при любом значении параметра) лежат в плоскости кривой 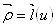 . Поэтому и все образующие лежат в этой плоскости, значит и поверхность является по определению поверхностью Каталана.
. Поэтому и все образующие лежат в этой плоскости, значит и поверхность является по определению поверхностью Каталана.
2) Предположим, что кривая 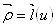 ВатАУ неплоская. По условию теоремы
ВатАУ неплоская. По условию теоремы 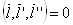 . Продифференцируем это равенство один раз по параметру:
. Продифференцируем это равенство один раз по параметру:
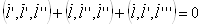
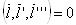 .
.
Если 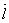 Ваколлинеарен вектору
Ваколлинеарен вектору 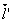 Вав некоторой точке. Тогда
Вав некоторой точке. Тогда
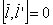
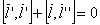
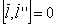
Значит 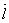 Ваколлинеарен
Ваколлинеарен  , а значит,
, а значит,  Ваколлинеарен и
Ваколлинеарен и 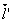 , а мы предположили противное, значит, этот случай невозможен, т.е.
, а мы предположили противное, значит, этот случай невозможен, т.е. 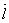 Ванеколлинеарен вектору
Ванеколлинеарен вектору 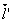 .
.
Посмотрим на картинку:

Так как 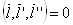 , то все эти три вектора лежат в одной плоскости тАУ плоскости
, то все эти три вектора лежат в одной плоскости тАУ плоскости 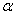 . А в силу того, что
. А в силу того, что 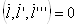 , эти векторы тоже лежат в одной плоскости тАУ плоскости
, эти векторы тоже лежат в одной плоскости тАУ плоскости 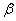 Ва(в первом случае плоскость обозначена двумя дугами, во втором, одной дугой). Так как векторы
Ва(в первом случае плоскость обозначена двумя дугами, во втором, одной дугой). Так как векторы 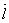 Ваи
Ваи  Ванеколлинеарны, то они в обоих случаях определяют плоскость, т.е. плоскости
Ванеколлинеарны, то они в обоих случаях определяют плоскость, т.е. плоскости 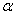 Ваи
Ваи 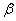 ВатАУ совпадают, а значит, все четыре вектора:
ВатАУ совпадают, а значит, все четыре вектора: 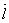 ,
, 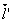 ,
,  ,
, 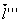 Валежат в одной плоскости, а значит:
Валежат в одной плоскости, а значит:  .
.
Напомним, что если дана кривая 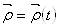 . То кручение кривой в точке
. То кручение кривой в точке 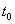 Вавычисляется по формуле:
Вавычисляется по формуле:
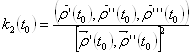 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (*)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (*)
Т.к.  ВатАУ то кривая
ВатАУ то кривая 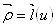 ВатАУ плоская, а это противоречит предположению пункта два. Т.е. рассматриваемая ситуация невозможна.
ВатАУ плоская, а это противоречит предположению пункта два. Т.е. рассматриваемая ситуация невозможна.
Таким образом, кривая 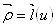 Ва(в условиях теоремы) может быть только плоской кривой и при этом поверхность является поверхностью Каталана ч.т.д.
Ва(в условиях теоремы) может быть только плоской кривой и при этом поверхность является поверхностью Каталана ч.т.д.
Замечание 2.3. Если в теореме убрать предположение о тройной непрерывной дифференцируемости вектор-функции 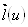 . То можно построить пример поверхности, такой что
. То можно построить пример поверхности, такой что 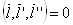 , но при этом поверхность не является поверхностью Каталана.
, но при этом поверхность не является поверхностью Каталана.
Красивый пример можно получить следующим образом.
Нам хочется, чтобы функция 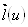 ВаВлразвернулаВ» плоскость прямых или разворачивала ее постоянно. Как следует из теоремы, соответствующую функцию следует искать среди функций, 3-яя производная которых терпит в какой-либо точке разрыв.
ВаВлразвернулаВ» плоскость прямых или разворачивала ее постоянно. Как следует из теоремы, соответствующую функцию следует искать среди функций, 3-яя производная которых терпит в какой-либо точке разрыв.
Например, можно задаться следующим уравнением: 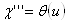 .
.
Здесь 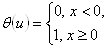 ВатАУ функция Хэвисайда.
ВатАУ функция Хэвисайда.
Проинтегрируем это уравнение.
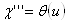
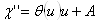
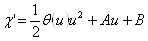
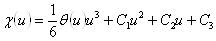 .
.
Теперь уже гораздо проще подобрать необходимый пример.
Итак, рассмотрим поверхность.
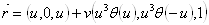
Проверим, что в каждой точке выполняется равенство: 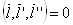 .
.
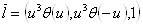
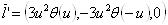
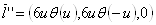
Замечание 4. Строго говоря, мы тут допустили неточность. А именно: 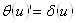 . Т.е. производная тета-функции Хэвисайда тАУ дельта-функция Дирака. Поэтому,
. Т.е. производная тета-функции Хэвисайда тАУ дельта-функция Дирака. Поэтому,
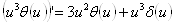 .
.
Однако, простое геометрическое рассуждение может убедить нас, что вторым слагаем можно пренебречь. Действительно, посмотрим на график функции:
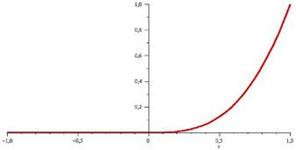
Очевидно, что в нуле наклон касательной к графику функции равен нулю, а функция 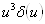 Варавна нулю всюду, кроме, быть может, нуля, следовательно, вклад в значение производной эта функция не вносит. Таким образом, Наше выражение для производной вполне корректно.
Варавна нулю всюду, кроме, быть может, нуля, следовательно, вклад в значение производной эта функция не вносит. Таким образом, Наше выражение для производной вполне корректно.
 .
.
Проверим условие коллинеарности векторов 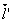 Ваи
Ваи  .
.
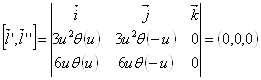
Как мы видим, они коллинеарны в каждой точке.
Теперь нам надо отыскать три прямые, которые вместе не лежат в параллельных плоскостях.
Для этого найдем три значения направляющего вектора этих прямых.
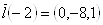 ,
,
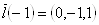 ,
,
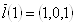
Если эти три вектора некомпланарны, то отвечающие им прямые (для которых они являются направляющими векторами) не лежат в параллельных плоскостях, т.е. являются искомыми.
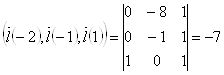 .
.
Т.е. эти прямые действительно не лежат в параллельных плоскостях.
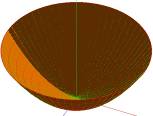
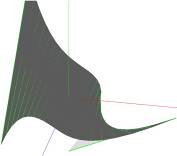
Ниже на рисунке изображен пример такой поверхности. Мы отчетливо видим, как на этой поверхности есть прямы, соответствующие данным векторам.
Более простой пример можно построить, убрав требование о том, что 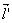 Ванеколлинеарен
Ванеколлинеарен  .
.
Найдем вектор, который в каждой точке обладает свойством, обратным к данному.
Пусть 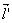 Ваколлинеарен вектору
Ваколлинеарен вектору 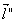 Вапри каждом значении параметра. Например:
Вапри каждом значении параметра. Например:
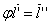
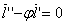
Пусть 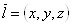 .
.
Решим уравнение, например, для координаты 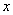 .
.
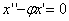
Сделаем замену: 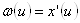 .
.
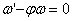
 .
.
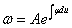 .
.
Подставим в 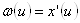 .
.
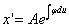
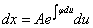
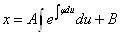 . Т.е.
. Т.е. 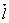 Ваимеет вид:
Ваимеет вид:
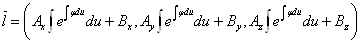
Вычислим производные для проверки.
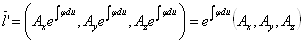 ,
,
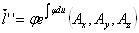 .
.
Теперь видно, что в каждой точке векторы 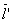 Ваи
Ваи  Ваколлинеарные, поэтому смешанное произведение будет заведомо равно нулю (другого и быть не могло, собственно).
Ваколлинеарные, поэтому смешанное произведение будет заведомо равно нулю (другого и быть не могло, собственно).
Теперь нам надо сделать так, чтобы нашлись 3 вектора 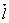 Ване лежащие в одной плоскости (при соответствующих значениях параметра).
Ване лежащие в одной плоскости (при соответствующих значениях параметра).
Т.е.
 ,
,
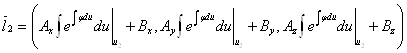 ,
,
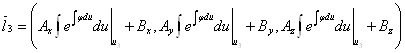 .
.
И при этом:  .
.
Поскольку сдвиг в пространстве всех этих трех векторов не повлияет на равенство (или не равенство) нулю смешанного произведения, то достаточно рассматривать векторы:
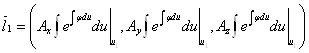 ,
,
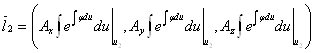 ,
,
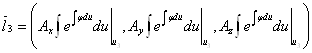 .
.
А эти векторы, очевидно, лежат в одной плоскости. Так что добиться выполнения утверждения о коллинеарности векторов 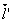 Ваи
Ваи  Вав каждой точке, при выполнении, которого поверхность не будет являться поверхностью Каталана тАУ нельзя.
Вав каждой точке, при выполнении, которого поверхность не будет являться поверхностью Каталана тАУ нельзя.
Значит, стоит подумать о примере, который обеспечивает выполнение этого условия в одной точке, в которой, разумеется, мы должны ВлповернутьВ» плоскость образующих линейчатой поверхности.
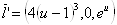
Рассмотрим вектор:
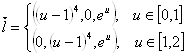
Очевидно:
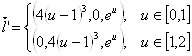 ,
,
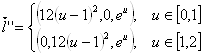

Очевидно, что 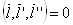 Вав каждой точке (есть нулевой столбец). Также, за исключением точки, соответствующей параметру
Вав каждой точке (есть нулевой столбец). Также, за исключением точки, соответствующей параметру 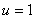 Вакручение вектора
Вакручение вектора 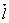 Ватакже равно нулю (
Ватакже равно нулю ( ). Причем, в каждой точке промежутка:
). Причем, в каждой точке промежутка: 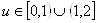
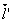 Ванеколлинеарен
Ванеколлинеарен  Ва(т.е. мы имеем право пользоваться формулой (*) для расчета кручения кривой на указанном промежутке).
Ва(т.е. мы имеем право пользоваться формулой (*) для расчета кручения кривой на указанном промежутке).
Действительно:
Если 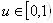 :
:  ,
, 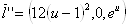 .
.
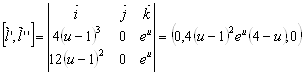
График ординаты имеет вид:
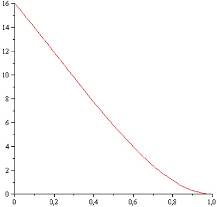
И мы видим, что он нигде кроме 1 в нуль не обращается (это видно и непосредственно из аналитического выражения).
Если  :
: 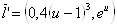 ,
, 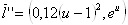 .
.
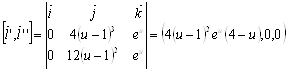
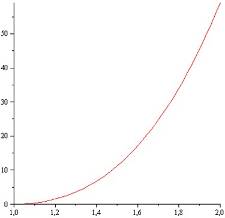
Аналогично тАУ график на данном полуинтервале:
Теперь мы уже поняли, что 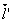 Ваколлинеарен
Ваколлинеарен  в точке
в точке 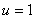 . Следовательно, вычислять кручение кривой в этой точке по формуле (*) нельзя. Как мы сейчас увидим, в результате тАУ кривая
. Следовательно, вычислять кручение кривой в этой точке по формуле (*) нельзя. Как мы сейчас увидим, в результате тАУ кривая 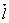 Ване будет плоской.
Ване будет плоской.
Действительно, возьмем три вектора:
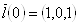 ,
,
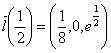 ,
,
 .
.
Проверим, лежат ли они в одной плоскости.
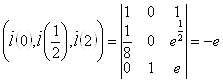 .
.
Действительно, они некомпланарны, а следовательно, и соответствующие этим векторам прямые не лежат
Вместе с этим смотрят:
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
Актуальные проблемы квантовой механики
Алгебра и алгебраические системы
Анализ эмпирического распределения
Аналитическая теория чисел. L-функция Дирихле