Статистика страхования
СОДЕРЖАНИЕ
1. СТАТИСТИКА СТРАХОВАНИЯ
1.1 Основные понятия статистики страхования
1.2 Статистика имущественного страхования
1.2.1 Основные абсолютные и относительные показатели
1.2.2 Расчет нетто-ставки
1.3 Статистика личного страхования
2. ПРАКТИЧЕСКОЕ ЗАДАНИЕ
ВЫВОДЫ
СПИСОК ЛИТЕРАТУРЫ
1. СТАТИСТИКА СТРАХОВАНИЯ
1.1 Основные понятия статистики страхования
Страхование представляет систему экономических отношений по защите имущественных и неимущественных интересов юридических и физических лиц путём формирования денежных фондов, предназначенных для возмещения ущерба и выплаты страховых сумм при наступлении страховых событий.
Страховое событие тАУ потенциальный страховой случай, на предмет которого производится страхование (несчастный случай, болезнь и т.п.).
Страховой случай тАУ это свершившееся страховое событие, с наступлением которого возникает обязанность страховщика произвести оплату страхователю.
При страховом случае с личностью страхователя выплата называется страховым обеспечением, а при страховом случае с имуществом - страховым возмещением.
1.2 Статистика имущественного страхования
Стихийные бедствия, их последствия и несчастные случаи нельзя предусмотреть в буквальном смысле. Закономерность этих событий можно проследить только в результате изучения массовой статистической информации, применяя соответствующие методы, основанные на теории вероятностей.
1.2.1 Основные абсолютные и относительные показатели
Основу системы показателей составляют характеристики, получаемые непосредственно из наблюдения. Применяемые в имущественном страховании показатели делятся на 3 группы: объёмные показатели, средние и относительные.
Основныеабсолютные показатели
| В· Страховое поле, максимальное число объектов, которое может быть охвачено страхованием | Nmax |
| В· Число застрахованных объектов, или число заключённых договоров страхования за определенный период(страховой портфель) | N |
| В· Страховая сумма застрахованного объекта | S |
| В· Сумма поступившего страхового платежа (страховой взнос) | V |
| В· Число страховых случаев | 
|
| В· Число пострадавших объектов | 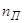
|
| В· Страховая сумма пострадавших объектов | 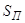
|
| В· Сумма выплаченного страхового возмещения | W |
Таблица 1.1. Основные относительные показатели имущественного страхования
Показатель | Формула расчета | Пояснения |
| Степень охвата страхового поля | 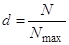
| Показывает долю застрахованных объектов от числа максимально возможных. Характеризует уровень развития добровольного страхования |
| Страховой платеж на 1 руб. страховой суммы | 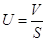
| Характеризует тарифную ставку страхования |
| Частота страховых случаев | 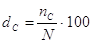
| Показывает, сколько страховых случаев приходится в расчёте на 100 или 1000 застрахованных объектов. Можно интерпретировать как вероятность гибели или повреждения застрахованного имущества. Всегда < 1. |
| Уровень опустошительности страхового случая (коэф-фициент кумуляции риска) | 
| Показывает, сколько объектов пострадало в одном страховом случае |
| Доля пострадавших объек-тов из числа застрахованных | 
| |
| Коэффициент выплат страхового возмещения (норма убыточности) | 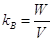
| Показывает, сколько копеек выплачивается в качестве страхового возмещения с каждого рубля страхового платежа. Если величина этого показателя >1, то страхование имущества убыточно. В динамике этот показатель должен уменьшаться. |
| Полнота уничтожения пострадавших объектов (коэффициент ущербности) | 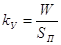
| Характеризует удельный вес суммы возмещения в страховой сумме пострадавших объектов. Если показатель равен 1, значит, в результате страхового случая ущерб равен действительной стоимости застрахованного имущества. Та-кой ущерб называется полным ущербом. Если  <1, ущерб называется частичным. <1, ущерб называется частичным. |
| Уровень убыточности страховых сумм | 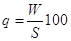
| Показывает, сколько рублей возмещается на каждый рубль страховой суммы |
Уровень убыточности страховых сумм - важнейший показатель имущественного страхования. Он зависит от:
В· количества заключённых договоров, N,
В· страховой суммы застрахованных объектов, S,
В· числа пострадавших объектов, 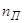 ,
,
В· полноты уничтожения застрахованных объектов,  ,
,
В· суммы выплат страхового возмещения, W.
Таким образом, он является результатом взаимодействия пяти из семи основных объемных показателей.
Таблица 1.2 Средние показатели по совокупности объектов используются для изучения производственной и хозяйственной деятельности страховых организаций:
Показатель | Формула расчета | Пояснения |
| Средняя страховая сумма застрахованного имущества |  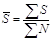
| |
| Средний размер страхового взноса | 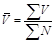
| |
| Среднее страховое возме-щение (средняя сумма страховых выплат) | 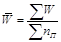
| |
| Средний уровень убыточ-ности страховых сумм | 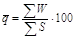
| Показатель должен быть < 1, т.к. иначе это означало бы недострахование. |
| Коэффициент тяжести страховых событий | 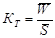
| Показывает, какая часть страховой суммы уничтожена |
| Средняя страховая сумма пострадавших объектов | 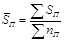
| |
| Средний показатель полно-ты уничтожения объектов (коэффициент ущербности) | 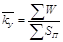
| 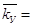 1 означает, что объек-ты полностью уничтожены. 1 означает, что объек-ты полностью уничтожены.
|
По данным текущей отчетности страховых компаний непосредственно исчислить можно лишь некоторые из перечисленных показателей (долю пострадавших объектов, показатель выплат страхового возмещения, уровень взносов по отношению к страховой сумме, показатель убыточности, а также средние величины). Для исчисления других показателей необходимо проведение специального статистического наблюдения, привлечение отчетности других организаций и ведомств (например, при исчислении показателя охвата страхового поля) или применение соответствующих статистических методов для возмещения неполноты учета.
Динамику среднего уровня убыточности можно изучать с помощью системы взаимосвязанных индексов переменного и постоянного состава, структурных сдвигов:
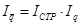 ,
,
 ,
,
где 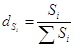 - доля (удельный вес) страховой суммы отдельных видов имущества в общей страховой сумме
- доля (удельный вес) страховой суммы отдельных видов имущества в общей страховой сумме
1.2.2 Расчет нетто-ставки
Одной из задач статистики в области страхования является обоснование уровня тарифной ставки.
Тарифная ставка тАУ ставка страхового платежа предназначена для возмещения ущерба, причинённого застрахованному имуществу страховым событием, а также для других расходов страховых организаций.
Тарифная ставка, которую называют брутто-ставкой, U, состоит из двух частей:
В· нетто-ставки, U', которая составляет 90-91 % от брутто-ставки,
В· и нагрузки (надбавки). Нагрузка устанавливается в % к брутто тАУ ставке, обычно составляет 9-11 % от нее.
U=U' + U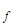 ,
,
где f тАУ доля нагрузки в брутто-ставке.
Брутто-ставка рассчитывается по формуле:
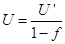
Нетто-ставка, U', составляет основную часть тарифа (ставки страхового платежа) и предназначена для создания фонда на выплату страхового возмещения. Обеспечивает возмещение убытков страхователей.
Нагрузка (надбавка) к нетто-ставке служит для образования резервных фондов содержания страховых органов, финансирования превентивных (предупреждение появления страховых событий) и репрессивных мероприятий (ликвидация наступивших последствий).
В основу расчёта нетто тАУ ставки, U', положен уровень убыточности имущества. Средний показатель убыточности рассчитывается по отчетным данным об убыточности за ряд лет:
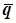 = Sq / ,
= Sq / ,
где - число лет,
или на основании данных о размерах страховых возмещений и о страховых суммах:
 .
.
Затем рассчитывается среднее квадратическое отклонение уровня убыточности от среднего значения:
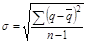
Для того, чтобы нетто-ставка отражала наиболее вероятную величину, к ней добавляется среднее квадратическое отклонение, умноженное на коэффициент доверительной вероятности. Таким образом, расчёт нетто-ставки производят по формуле:
U' = 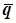 + t,
+ t,
где t - коэффициент доверия в соответствии с принятой вероятностью наступления страховых событий (коэффициент Лапласа).
1.3 Статистика личного страхования
Расчеты в личном страховании основаны на таблицах смертности и средней продолжительности жизни населения и показателях доходности.
В таблице смертности используются одногодичные возрастные группы от 0 (новорожденные) до 100 лет.
Таблица 1.3. Макет таблицы смертности и средней продолжительности жизни
| Возраст, лет | Число доживающих до возраста X лет | Число умирающих при переходе от возраста X к возрасту X+1 | Вероятность умереть в возрасте от X до X+1 год | Вероятность дожить до возраста X+1 |
X | LX | dX | 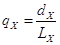
| 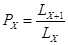
|
X+1 | | | | |
Вероятность умереть в течение предстоящего года жизни, т.е. при переходе от возраста X к возрасту X+1 рассчитывается:
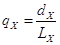
Вероятность дожить до следующего возраста можно определить как
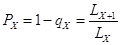
Средний показатель доходности за период рассчитывается по стране в целом или как средняя арифметическая взвешенная по доходам от инвестиций конкретной страховой компании за предыдущие периоды:
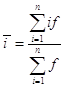 ,
,
где i тАУ доходность по отдельному виду инвестиций, в долях от 1,
f тАУ объем инвестиций,
n тАУ число инвестиционных проектов.
Расчет нетто-ставки при страховании лица в возрасте Х лет на дожитие n лет:
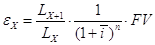 ,
,
где 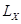 - число лиц в начале срока страхования (из таблицы смертности),
- число лиц в начале срока страхования (из таблицы смертности),
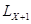 - число лиц, доживших до конца срока страхования (из таблицы смертности),
- число лиц, доживших до конца срока страхования (из таблицы смертности),
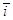 - средняя доходность за период действия договора,
- средняя доходность за период действия договора,
FV тАУсумма страхового обеспечения,
тАУ срок договора страхования.
2. ПРАКТИЧЕСКОЕ ЗАДАНИЕ
Исходные данные
Таблица 2.1. Показатели деятельности предприятия за отчётный период
| № предприятия | Объём производства, тонн | Среднегодовая стоимость основных производственных фондов, млн. руб. |
| А | 1 | 2 |
| 1 | 978 | 3,52 |
| 2 | 1043,6 | 3,71 |
| 3 | 620,6 | 2,13 |
| 4 | 485,1 | 1,05 |
| 5 | 884,5 | 2,82 |
| 6 | 1020,4 | 4,1 |
| 7 | 872,3 | 2,73 |
| 8 | 421,8 | 1,5 |
| 9 | 280,6 | 0,89 |
| 10 | 851,8 | 3,04 |
| 11 | 637,2 | 2,37 |
| 12 | 815,6 | 2,56 |
| 13 | 921,7 | 3,2 |
| 14 | 544,3 | 1,64 |
| 15 | 915,1 | 3 |
| 16 | 1010,4 | 3,61 |
1. Для того, чтобы провести аналитическую группировку с равными интервалами, необходимо определить оптимальное число групп, которое рассчитывается по формуле Стержесса:
m=1+3,321В·lgN, (1)
где m тАУ число групп, N тАУ число единиц совокупности.
m=1+3,321В·lg16=4,999.
Так как число групп должно быть целым, то выбираем m=5.
2. В качестве признака, по которому строится группировка, берётся факторный признак х тАУ объём производства, от которого зависит результативный признак у тАУ среднегодовая стоимость основных производственных фондов.
Зная число групп, рассчитываем величину интервала:
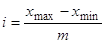 (2)
(2)
Величина интервала составляет:
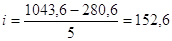
Таблица 2.2. Вспомогательная таблица для построения группировки предприятий по объёму производства
| № группы | Группы предприятий по объёму производства, тонн | Номера предприятий, входящих в группу |
| 1 | 280,6 тАУ 433,2 | 8, 9 |
| 2 | 433,2 тАУ 585,8 | 4, 14 |
| 3 | 585,8 тАУ 738,4 | 3, 11 |
| 4 | 738,4 тАУ 891 | 5, 7, 10, 12 |
| 5 | 891 тАУ 1043,6 | 1, 2, 6, 13, 15, 16 |
На основании вспомогательной таблицы (таблица 2) и таблицы исходных данных (таблица 1), построим аналитическую группировку и представим её в статистической таблице (таблица 3).
Таблица 2.3. Аналитическая группировка предприятий по объёму производства для выявления взаимосвязи между показателями: объём производства и среднегодовой стоимости основных производственных фондов
| Группы предприятий по объёму производства, тонн | Количество предприятий, ед. | Удельный вес Группы предприятий, % | Объём производства, тонн | Среднегодовая стоимость основных производственных фондов, млн. руб. | |
| |
| итого | в среднем | итого | в среднем | |
| А | 1 | 2 | 3 | 4 | 5 | 6 | |
| 280,6 тАУ 433,2 | 2 | 12,5 | 702,4 | 351,2 | 2,39 | 1,195 | |
| 433,2 тАУ 585,8 | 2 | 12,5 | 1029,4 | 514,7 | 2,69 | 1,345 | |
| 585,8 тАУ 738,4 | 2 | 12,5 | 1257,8 | 628,9 | 4,5 | 2,25 | |
| 738,4 тАУ 891 | 4 | 25 | 3424,2 | 856,05 | 11,15 | 2,788 | |
| 891 тАУ 1043,6 | 6 | 37,5 | 5889,2 | 981,53 | 21,14 | 3,523 | |
Итого: | 16 | 100 | 12303 | | 41,87 | | |
В среднем: | | | | 768,94 | | 2,617 | |
В представленной таблице 3 показатель ВлУдельный вес группы предприятийВ» [УВ] для графы 2 рассчитывается на основании формулы:
 , (3)
, (3)
где f тАУ частота i-ой группы, т.е. количество предприятий в каждой группе.
Из таблицы видно, что наибольший удельный вес имеет 5 группа тАУ 37,5 %. При этом наблюдается рост среднего значения объёма производства и среднегодовой стоимости основных производственных фондов, что говорит о возможном наличии между данными положительной связи.
3. Для того, чтобы построить гистограмму распределения и кумуляту создадим вспомогательную таблицу.
Таблица 2.4. Вспомогательная таблица для построения графических характеристик
| Группы предприятий по объёму производства, тонн | f, ед | , ед. |
| А | 1 | 2 |
| 280,6 тАУ 433,2 | 2 | 2 |
| 433,2 тАУ 585,8 | 2 | 4 |
| 585,8 тАУ 738,4 | 2 | 6 |
| 738,4 тАУ 891 | 4 | 10 |
| 891 тАУ 1043,6 | 6 | 16 |
Итого: | 16 | |
В таблице 4 в графе 2, представлена накопленная частота [s], которая показывает, сколько единиц совокупности имеют значения признака не больше, чем данное значение. Данный показатель вычисляется путём последовательного прибавления к частоте первого интервала частот последующих интервалов.
На рисунках 1 и 2 представлены соответственно гистограмма распределения и кумулята

Рис. 2.1. Гистограмма распределения
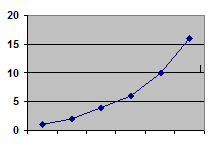
Рис. 2.2. Кумулята
При построении гистограммы (рис.1) на оси абсцисс (х) откладываются величины интервалов, а частоты изображаются прямоугольниками, построенными на соответствующих интервалах. Высота столбцов должна быть пропорциональна частотам.
При построении кумуляты (рис.2) интервального вариационного ряда по оси абсцисс (х) откладываются варианты ряда, а по оси ординат () накопленные частоты, которые наносят на поле графика в виде перпендикуляров к оси абсцисс в верхних границах интервалов. Затем эти перпендикуляры соединяют и получают ломаную линию, то есть кумуляту.
4. Факторный признак тАУ объём производства. Среднее значение для данного признака можно определить двумя способами:
1 способ тАУ для несгруппированных данных, с помощью простой средней:
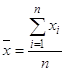 , (4)
, (4)
где тАУ количество значений ряда наблюдения.
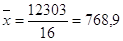 тонн
тонн
2 способ тАУ для вариационного ряда (таблица 3) с помощью формулы взвешенной средней:
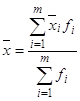 , (5)
, (5)
где  тАУ среднее значение i-ой группы, m тАУ число групп.
тАУ среднее значение i-ой группы, m тАУ число групп.
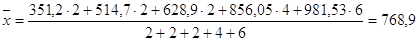 тонн
тонн
Размах вариации [R] зависит от величины только двух крайних вариант и не учитывает степени колеблемости основной массы членной ряда:
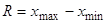 , (6)
, (6)
где 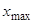 ,
, 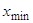 тАУ соответственно максимальное и минимальное значение признака.
тАУ соответственно максимальное и минимальное значение признака.
Размах вариации составляет:
R=1043,6 тАУ 280,6 = 763
Среднее линейное отклонение, дисперсия и среднее квадратическое отклонение можно определить двумя способами.
Среднее линейное отклонение:
В· для первичного ряда:
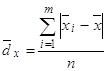 (7)
(7)
В· для вариационного ряда:
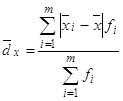 (8)
(8)
Дисперсия:
В· для первичного ряда:
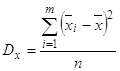 (9)
(9)
В· для вариационного ряда:
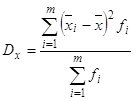 (10)
(10)
Среднее квадратическое отклонение:
В· для первичного ряда:
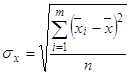 (11)
(11)
В· для вариационного ряда:
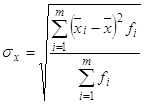 (12)
(12)
Используем способ вариационного ряда. Для расчёта по формулам (8), (10), (12) целесообразно построить вспомогательную таблицу расчёта.
Таблица 2.5. Вспомогательная таблица для расчёта показателей вариации
| Группы предприятий по объёму производства, тонн |  , ,
тонн | 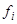 , ,
ед. | 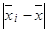 , ,
тонн |  , ,
тонн | 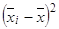 , ,
тонн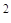 | 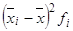 , ,
тонн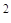 |
| А | 1 | 2 | 3 | 4 | 5 | 6 |
| 280,6 тАУ 433,2 | 351,2 | 2 | 417,7 | 835,48 | 174504,6 | 349009,2 |
| 433,2 тАУ 585,8 | 514,7 | 2 | 254,2 | 508,48 | 64636,7 | 129273,4 |
| 585,8 тАУ 738,4 | 628,9 | 2 | 140,03 | 280,08 | 19610,5 | 39221 |
| 738,4 тАУ 891 | 856,05 | 4 | 87,11 | 348,45 | 7588,6 | 30354,4 |
| 891 тАУ 1043,6 | 981,533 | 6 | 212,6 | 1275,58 | 45196,97 | 271181,8 |
Итого: | | 16 | | 3248,05 | | 819039,8 |
На основании таблицы 5, получаем:
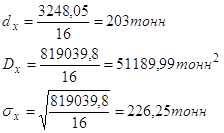
Зная среднее квадратическое отклонение и среднее значение признака, определяется коэффициент вариации:
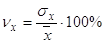 , (13)
, (13)
Получаем,
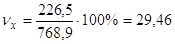 %
%
Так как коэффициент вариации превышает 25%, то вариация объёма производства сильная. Так как коэффициент вариации не превышает 33%, то это говорит об однородности информации.
5. В основе дисперсионного анализа лежит разделение дисперсии на части или компоненты. Данный анализ сводится к расчёту и анализу трёх видов дисперсий: общей, внутригрупповой и межгрупповой. Общая дисперсия 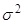 измеряет вариацию результативного признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Данный вид дисперсии рассчитывается на основании исходных несгруппированных данных по формуле:
измеряет вариацию результативного признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Данный вид дисперсии рассчитывается на основании исходных несгруппированных данных по формуле:
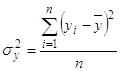 , (14)
, (14)
Для расчёта по формуле (14) построим вспомогательную таблицу расчёта.
Таблица 2.6 Вспомогательная таблица для расчёта общей дисперсии
| № п/п |  , ,
тонн | 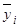 , ,
млн. руб. | 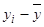 , млн. руб. , млн. руб.
| 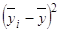 , ,
(млн. руб)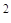 |
| А | 1 | 2 | 3 | 4 |
| 1 | 978 | 3,52 | 0,9 | 0,81 |
| 2 | 1043,6 | 3,71 | 1,09 | 1,19 |
| 3 | 620,6 | 2,13 | -0,49 | 0,24 |
| 4 | 485,1 | 1,05 | -1,57 | 2,46 |
| 5 | 884,5 | 2,82 | 0,2 | 0,04 |
| 6 | 1020,4 | 4,1 | 1,48 | 2,19 |
| 7 | 872,3 | 2,73 | 0,11 | 0,01 |
| 8 | 421,8 | 1,5 | -1,12 | 1,25 |
| 9 | 280,6 | 0,89 | -1,73 | 2,99 |
| 10 | 851,8 | 3,04 | 0,42 | 0,18 |
| 11 | 637,2 | 2,37 | -0,25 | 0,06 |
| 12 | 815,6 | 2,56 | -0,06 | 0,004 |
| 13 | 921,7 | 3,2 | 0,58 | 0,34 |
| 14 | 544,3 | 1,64 | -0,98 | 0,96 |
| 15 | 915,1 | 3 | 0,38 | 0,14 |
| 16 | 1010,4 | 3,61 | 0,99 | 0,98 |
Итого | 12303 | 41,87 | | 13,86 |
Среднее | 768,94 | 2,62 | | 0,866 |
На основании таблицы 6 определяем:
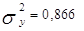 (млн. руб)
(млн. руб)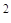
Межгрупповая дисперсия 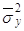 характеризует систематическую вариацию под воздействие признака тАУ фактора, положенного в основание группировки. Она является мерой вариации частных средних по группам
характеризует систематическую вариацию под воздействие признака тАУ фактора, положенного в основание группировки. Она является мерой вариации частных средних по группам 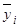 вокруг общей средней
вокруг общей средней  и определяется по формуле:
и определяется по формуле:
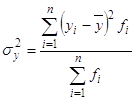 (15)
(15)
Для расчёта по формуле (12) построим вспомогательную таблицу расчёта.
Таблица 2.7 Вспомогательная таблица для расчёта межгрупповой дисперсии
| Группы предприятий по объёму производства, тонн | 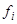 , ,
ед. | 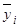 , ,
млн. руб. | 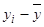 , млн. руб. , млн. руб.
| 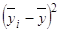 , ,
(млн. руб)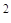 |  , ,
(млн. руб)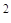 |
| А | 1 | 2 | 3 | 4 | 5 |
| 280,6 тАУ 433,2 | 2 | 1,195 | -1,425 | 2,03 | 4,06 |
| 433,2 тАУ 585,8 | 2 | 1,345 | -1,275 | 1,63 | 3,25 |
| 585,8 тАУ 738,4 | 2 | 2,25 | -0,37 | 0,14 | 0,27 |
| 738,4 тАУ 891 | 4 | 2,788 | 0,168 | 0,03 | 0,11 |
| 891 тАУ 1043,6 | 6 | 3,523 | 0,903 | 0,82 | 4,89 |
Итого: | | | | | 12,59 |
В среднем: | | | | | 0,787 |
На основании таблицы 7 определяем:

Вариацию, обусловленную влиянием прочих факторов, характеризует в каждой группе внутригрупповая дисперсия 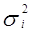 :
:
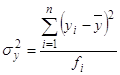 , (16)
, (16)
Соответственно внутригрупповая дисперсия 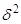 определяется путём суммирования отдельных внутригрупповых дисперсий, взвешенных по частоте.
определяется путём суммирования отдельных внутригрупповых дисперсий, взвешенных по частоте.
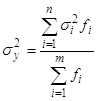 , (17)
, (17)
Для расчёта общей внутригрупповой дисперсии построим вспомогательную таблицу расчёта:
Таблица 2.8 Вспомогательная таблица для расчёта внутригрупповой дисперсии
Группы предприятий по объёму производства, тонн | № предприятий, входящих в группу | 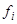 , ,
ед. |  , млн. руб. , млн. руб.
| 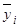 , ,
млн. руб. | 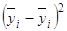 , ,
(млн. руб.)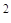 | 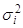 , ,
(млн. руб.)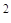 | 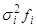 , ,
(млн. руб.)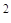 |
| 280,6 тАУ 433,2 | 8 | 2 | 1,5 | 1,195 | 0,0930 | 0,093 | 0,186 |
| 9 | 0,89 | 0,0930 |
| 433,2 тАУ 585,8 | 4 | 2 | 1,05 | 1,345 | 0,087 | 0,087 | 0,174 |
| 14 | 1,64 | 0,087 |
| 585,8 тАУ 738,4 | 3 | 2 | 2,13 | 2,25 | 0,014 | 0,014 | 0,029 |
| 11 | 2,37 | 0,014 |
| 738,4 тАУ 891 | 5 | 4 | 2,82 | 2,788 | 0,001 | 0,0299 | 0,1199 |
| 7 | 2,73 | 0,003 |
| 10 | 3,04 | 0,064 |
| 12 | 2,56 | 0,052 |
| 891 тАУ 1043,6 | 1 | 6 | 3,52 | 3,523 | 0 | 0,126 | 0,753 |
| 2 | 3,71 | 0,035 |
| 6 | 4,1 | 0,339 |
| 13 | 3,2 | 0,104 |
| 15 | 3 | 0,274 |
| 16 | 3,61 | 0,008 |
Итого: | | 16 | 41,87 | | | | 1,26 |
В среднем: | | | | | | | 0,079 |
На основании таблицы 8 определяем:
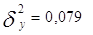 (млн. руб.)
(млн. руб.)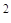
Для проверки правильности найденных дисперсий воспользуемся правилом сложения дисперсий, согласно которому:
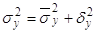 (18)
(18)
Подставим найденные значения в формулу (18):
0,866=0,787+0,079 (млн. руб.)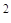
0,866=0,866 (млн. руб.)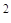
Так как правило сложения дисперсий выполняется, то рассчитанные значения дисперсий определены верно.
Определим силу влияния группировочного признака на образование общей вариации, рассчитав эмпирический коэффициент детерминации 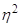 :
:
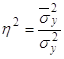 , (19)
, (19)
Получаем:
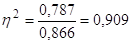
Так как полученный эмпирический коэффициент детерминации близок к единице, то это говорит о том, что связь между рассматриваемыми признаками достаточно сильная.
Эмпирическое корреляционное отношение определяется по формуле:
 (20)
(20)
Получаем:
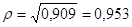
Так как 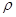 >0,7, связь между признаками объём реализации и среднегодовая стоимость основных производственных фондов тАУ сильная.
>0,7, связь между признаками объём реализации и среднегодовая стоимость основных производственных фондов тАУ сильная.
6. В рамках корреляционного анализа решается задача обнаружения линейной связи и оценки её уровня. Самый простой способ оценки связи тАУ это графический способ. В этом случае строится поле корреляции, которое образует множество точек с координатами (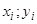 ), i=1, .. N.
), i=1, .. N.
По виду корреляционного поля можно оценить
Вместе с этим смотрят:
РЖнвестицiйна дiяльнiсть комерцiйного банку та ii вплив на його фiнансовий стан
РЖнвестицiйна полiтика банкiв в Украiнi
РЖнкорпорацiя та консолiдацiя як первиннi форми систематизацii банкiвського законодавства Украiни
РЖнструменти пiдтримки платоспроможностi та лiквiдностi комерцiйного банку (на прикладi АКБ "Приватбанк")
РЖпотечне кредитування як механiзм залучення фiнансових ресурсiв для пiдприiмницькоi дiяльностi