Изучение истории становления и развития методики преподавания математики в России
Актуальность темы исследования. Отечественное математическое образование прошло длинный путь. Этапы его становления и развития интересны и весьма поучительны.
В настоящее время ведется поиск оптимального содержания математического образования. Это объясняется тем, что с начала 90-х годов прошлого века и до настоящего времени происходит непрерывное реформирование школы, которое пока не привело к каким-либо заметным положительным результатам. В течение этого времени наша школа находится на распутье: с одной стороны, она стремится к обновлению, с другой, пытается сохранить свои лучшие традиции.
Именно для того чтобы осознать настоящие и предвосхитить грядущие проблемы математического образования, вызванные в частности, модернизацией школы, необходимо представить общую и целостную картину развития математического образования в России, а для этого нужно обратиться к его периодизации.
К сожалению, в настоящее время еще нет устоявшегося подхода к определению периодизации развития математического образования.
Ряд исследователей, таких как Ю.М. Колягин, Т.С. Полякова, О.А. Саввина, О.В. Тарасова, Р.С. Черкасов, в своих работах предлагают разные подходы к периодизации развития математического образования. В научных работах И.К. Андронова и Р.С. Черкасова предприняты попытки определить не только периодизацию математического образования, но и периодизацию методики преподавания математики как науки.
Первые сведения об учении детей простейшим вычислениям встречаются в источниках по истории стран Древнего Востока. Большое влияние на развитие школьного математического образования оказала математическая культура Древней Греции, где уже в 5 веке до н.э. в связи с развитием торговли, мореплавания, ремёсел в начальной школе изучались счёт и практическая геометрия.
Содержание учебного предмета математики меняется со временем в связи с расширением целей образования, появления новых требований к школьной подготовке, изменением стандартов образования.
История отечественного математического образования является общенациональным достоянием и требует к себе крайне бережного отношения. Это отношение к ней независимо от времени должно носить в большей степени ВлмонументальныйВ» и ВлантикварныйВ» характер, нежели ВлкритическийВ». Между тем нередко работы советских историков, посвященные дооктябрьскому периоду, в силу принятых в то время идеологических установок, носили преимущественно критический оттенок в противоположность апологетическому описанию развития математического образования в советское время. Поэтому остро встает проблема необходимости целостного и объективного исследования истории математического образования в школе России.
Предмет исследования: методика преподавания математики как науки;
Объект исследования: история развития и становления методики преподавания математики в России;
Цель исследования: изучение истории становления и развития методики преподавания математики в России.
Задачи исследования:
- изучение литературы по теме исследования;
- исследование методического и исторического подходов к проблеме исследования;
- анализ методики преподавания математики как науки;
- изучение исторических аспектов методики преподавания математики в России;
- анализ методики преподавания математики в начальной школе;
- изучение направлений преподавания математики на современном этапе;
Методы исследования: изучение литературы, сравнение, теоретический анализ и синтез, наблюдение;
Глава 1. Теоретические аспекты изучения проблемы исторического становления и развития методики преподавания математики в России
1.1 Исторические и методические аспекты проблемы преподавания математики в России
математика алгебра аналитический геометрия
Долгое время история математического образования не являлась специальным объектом научных исследований, и ее отдельные грани освещались либо в рамках истории развития различных учебных заведений, либо в контексте истории математики, либо на фоне материалов, посвященных персоналиям. Поэтому отрадно отметить, что на рубеже XX-XXI веков выходят фундаментальные работы по истории обучения математике в России Ю.М.Колягина и Т.С.Поляковой[3].
Несмотря на уникальность этих сочинений, все же следует отметить, что, вследствие поставленных авторами задач, они описывают историю отечественного математического образования в целом. Между тем не в меньшей степени представляется интересной история преподавания конкретных дисциплин: арифметики, алгебры, геометрии и т.д. Тем более важно исследовать эволюцию обучения высшей математике в школе, поскольку наличие этого раздела в школьном курсе на протяжении столетий вызывает у педагогов наибольшее количество споров. Даже сегодня представляется весьма затруднительным получить однозначные и исчерпывающие ответы на традиционные вопросы: ВлНужна ли высшая математика в школе?В», ВлКакие вопросы высшей математики должны найти отражение в школьной программе?В», ВлКаким образом осуществить введение элементов высшей математики в школу?В» и, наконец, ВлКак при этом эффективно организовать процесс обучения?В». Но, несмотря на различие мнений, элементы высшей математики уже стали неотъемлемой частью школьного курса математики.
Надо признать, что деление математики на высшую и элементарную весьма условно. Действительно, одним из важнейших объектов курса высшей математики являются функции, которые параллельно могут рассматриваться и в курсе элементарной математики. Более существенным является различие методов исследования функций (в отличие от элементарной, высшая математика широко использует понятие предела, производной и интеграла). Исторически термин Влвысшая (ВлвышняяВ») математикаВ» начал употребляться еще в XVIII в. (Хр.Вольф, П.И. Гиларовский и др.) для обозначения двух разделов: аналитической геометрии и анализа бесконечно малых чисел. В настоящее время в Математическом энциклопедическом словаре высшая математика определяется несколько шире - как Влсовокупность математических дисциплин, входящих в учебный план технических и некоторых других учебных заведенийВ». В случае такой интерпретации курс высшей математики образуют элементы аналитической геометрии, линейной алгебры, дифференциального и интегрального исчислений, теории дифференциальных уравнений. Как видим, содержание предмета высшей математики за прошедшие двести лет претерпело определенные изменения.
Детальный анализ историко-педагогической и методико-математической литературы позволяет утверждать, что приводимые в ней сведения не дают даже общей картины постановки преподавания элементов высшей математики в XVIII-XX вв. как в высшей, так и в средней школе; все эти сведения весьма разрозненны, не систематизированы, имеют расхождения в датах, описании фактов, оценке событий. Требуют уточнения, к примеру, многочисленные факты о жизни и научной деятельности таких педагогов-математиков, как С.К.Котельников, М.Г.Попруженко и многих др.; имеют место разночтения в сроках и причинах проникновения элементов высшей математики в школьный курс; встречается переоценка роли педагогов Влв борьбеВ» за внедрение идей высшей математики в среднюю школу и т.п[12].
Сказанное во многом можно отнести и к другим разделам школьного курса математики. Таким образом, есть все основания констатировать, что в настоящее время обострились противоречия между:
- сохранением традиций отечественной системы математического образования и необходимостью ее обновления, вызванного требованиями времени (в т.ч. в контексте модернизации средней школы);
- фактическим проникновением элементов высшей математики в школьный курс и отсутствием единой теории, обосновывающей необходимость изучения высшей математики в средней школе;
- историко-культурной и педагогической потребностью в осмыслении исторического опыта обучения высшей математике в средней школе и недостатком знаний об этом важном разделе истории математического образования (в т.ч. недостаточной его освещенностью в научных исследованиях).
История развития математики тАУ это не только история развития математических идей, понятий и направлений, но это и история взаимосвязи математики с человеческой деятельностью, социально-экономическими условиями различных эпох.
Становление и развитие математики как науки, возникновение ее новых разделов тесно связано с развитием потребностей общества в измерениях, контроле, особенно в областях аграрной, промышленной и налогообложения. Первые области применения математики были связаны с созерцанием звезд и земледелием. Изучение звездного неба позволило проложить торговые морские пути, караванные дороги в новые районы и резко увеличить эффект торговли между государствами. Обмен товарами приводил к обмену культурными ценностями, к развитию толерантности как явления, лежащего в основе мирного сосуществования различных рас и народов. Понятие числа всегда сопровождалось и нечисловыми понятиями. Например, один, два, многотАж Эти нечисловые понятия всегда ограждали сферу математики. Математика придавала законченный вид всем наукам, где она применялась. В Европе сложилось разделение на гуманитарные и естественные науки по степени влияния математики на эти части.
Перед преподаванием математики в школе кроме общих целей обучения стоят ещё свои специфические цели, определяемые особенностями математической науки. Одна из них тАУ это формирование и развитие математического мышления. Это способствует выявлению и более эффективному развитию математических способностей школьников, подготавливает их к творческой деятельности вообще и в математике с ее многочисленными приложениями в частности.
Вообще интеллектуальное развитие детей можно ускорить по трём направлениям: понятийный строй мышления, речевой интеллект и внутренний план действий.
Прочное усвоение знаний невозможно без целенаправленного развития мышления, которое является одной из основных задач современного школьного обучения.
Хочется обратить внимание на две главные проблемы дидактики математики: модернизация содержания школьного математического образования и совершенствование структуры курса.
Быстрый рост объема научной информации, ограниченность срока школьного обучения и невозможность сокращения объема изучаемых в школе основ науки с целью включения новой информации усложняют проведение реформ по модернизации школьного образования, а поэтому готовить их придется в течение более длительного времени, тщательно и строго на научной основе.
Имеют место успешные эксперименты по модернизации курса начальных классов и изучению в нем начал алгебры, что позволило дать значительную пропедевтику алгебры и геометрии в I-V классах, позволяющую изучить систематические курсы этих предметов в более быстром темпе и перенести ряд тем из старших классов в средние; включить в программу старших классов элементы высшей математики. Таким образом, улучшение системы курса возможно и в период между реформами, т.е. независимо от модернизации образования.
1.2 Методика преподавания математики как наука. Основные вопросы изучения
Слово ВлметодикаВ» в переводе с древнегреческого означает Влспособ познанияВ», Влпуть исследованияВ». Метод - это способ достижения какой-либо цели, решения конкретной учебной задачи.
Существуют разные точки зрения на содержание понятия ВлметодикаВ». Одни, признавая методику наукой педагогической, рассматривали ее как частную дидактику с общими для всех предметов принципами обучения. Другие считали методику специальной педагогической наукой, решающей все задачи обучения и развития личности через содержание предмета. Приведем несколько примеров определений.
Методика преподавания математики - наука о математике как учебном предмете и закономерностях процесса обучения математике учащихся различных возрастных групп и способностей.
Методика обучения математике тАУ это педагогическая наука о задачах, содержании и методах обучения математике. Она изучает и исследует процесс обучения математике в целях повышения его эффективности и качества. Методика обучения математике рассматривает вопрос о том, как надо преподавать математику.
Методика преподавания математики - раздел педагогики, исследующий закономерности обучения математике на определенном уровне ее развития в соответствии с целями обучения подрастающего поколения, поставленными обществом. Методика обучения математике призвана исследовать проблемы математического образования, обучения математике и математического воспитания. Методика преподавания математики тАУ педагогическая наука и, соответственно, учебная дисциплина, исследующая закономерности обучения математики вообще, закономерности обучения математике в школе в частности (5), наука о математике как учебном предмете и закономерностях процесса обучения математике учащихся различных возрастных групп на определенном уровне её развития в соответствии с целями обучения, поставленными обществом[14] .
Методика преподавания математики занимается, прежде всего, изучением, разработкой, усовершенствованием различных методов и форм преподавания математики в школах, а также многообразными организационными вопросами, возникающими при применении этих методов и форм на практике. Эта дисциплина выясняет, как обеспечить прочные систематизированные знания и навыки в объеме, установленном программой, тратя на это минимум времени и сил, и как обеспечить достижение тех воспитательных целей, какие ставит себе изучение математики. Методика преподавания математики изучает и систематизирует опыт лучших учителей и даёт возможность начинающему учителю избежать многих ошибок, легко допускаемых на первых порах и приводящих к большим потерям для учащихся. Исходя из конкретных задач, стоящих перед учителем математики, имеющим класс с определенным составом учащихся, определенную программу, определенные учебники, твердое расписание, методика устанавливает способы наилучшего использования всех этих конкретных условий для достижения поставленной цели. Кроме того, она накопляет также опыт учителей, говорящий о желательности тех или иных изменений в учебных планах, программах, учебниках.
Методика математики тАУ наука, выводы которой немедленно и самым широким образом применяются на практике и являются базой искусства преподавания [13].
Методика преподавания математики прежде всего должна ответить на несколько основных, тесно связанных между собой вопросов.
Первый из них тАУ зачем обучать математике? Очевидно, ответ на этот вопрос можно получить, исходя из общих задач воспитания, которые, в свою очередь, определяются задачами, стоящими перед обществом на соответствующем этапе его развития.
Второй вопрос тАУ кого обучать математике? С одной стороны, это вопрос о возрасте: когда целесообразно приступать к обучению детей математике и когда следует заканчивать изучение обязательной для всех программы? С другой стороны это приобретающий все большую актуальность вопрос о ВлпослешкольномВ» продолжении математического образования.
Третий вопрос тАУ каково содержание изучаемого курса математики? Ответ на этот вопрос теснейшим образом связан с ответом на вопрос о целях обучения математике. Следует подчеркнуть, что, пожалуй, именно в математике вопрос о том, что именно и в каком объеме следует отобрать из сегодняшней науки для школьной программы, является наиболее сложным, важным и спорным.
Наконец, четвертый вопрос тАУ как обучать математике? Очевидно, что ответ на этот вопрос и составляет важнейшую часть курса методики преподавания математики, причем материал этот является наиболее подвижным, наиболее конкретным, наиболее близким учителю-практику, требует к себе поистине творческого отношения.
Дидактика математики относится к группе педагогических наук и находится в тесной связи с педагогикой. Влияние на нее оказывают и математические науки. Также методика математики основывается на понятиях и законах психологии. Физиология высшей нервной деятельности, в частности учение И.П. Павлова об условных рефлексах, находит применение в обучении математике. Плодотворное влияние на дидактику математики оказывает связь логикой, историей математики, с ее историей.
Методика преподавания математики рассматривает такие вопросы, как цели обучения, математические понятия и предложения, теоремы и их доказательство, задачи и их решение, методы и формы обучения, урок по математике и др[6].
Методика преподавания математики в школе возникла с целью поиска педагогически целесообразных путей и способов изложения учебного материала. Методика преподавания математики начала разрабатываться чешским учёным Я.А. Коменским. Методика обучения математике впервые выделилась как самостоятельная дисциплина в книге швейцарского учёного И.Г. Песталоцци ВлНаглядное учение о числеВ» (1803, русский перевод 1806). Первым пособием по методике математики в России стала книга Ф.И. Буссе ВлРуководство к преподаванию арифметики для учителейВ» (1831). Создателем русской методики арифметики для народной школы считается П.С. Гурьев, который критерием правильности решения методических проблем признавал опыт и практику.
Цель методики обучения математике заключается в исследовании основных компонентов системы обучения математике в школе и связей между ними. Под основными компонентами понимаются: цели, содержание, методы, формы и средства обучения математике.
Предмет методики обучения математике отличается исключительной сложностью. Предметом методики обучения математике является обучение математике, состоящее из целей и содержания математического образования, методов, средств, форм обучения математике. На функционирование системы обучения математике оказывает влияние ряд факторов: общие цели образования, гуманизация и гуманитаризация образования, развитие математики как науки, прикладная и практическая направленность математики, новые образовательные идеи и технологии, результаты исследований в психологии, дидактике, логике и т.д. Совокупность этих факторов образует внешнюю среду, которая оказывает непосредственное влияние на систему обучения математике. Многие компоненты внешней среды воздействуют на нее через цели обучения математике.
Методика преподавания математики претерпевает в своем развитии большие трудности, прежде всего, из-за сложностей преодоления разрыва между школьной математикой и математической наукой, а также из-за того, что она является пограничным разделом педагогики на стыке философии, математики, логики, психологии, биологии, кибернетики и, кроме того, искусства[13].
Глава 2. Стадии становления методики преподавания математики в России
2.1 Основные периоды и этапы становления методики преподавания математики в России
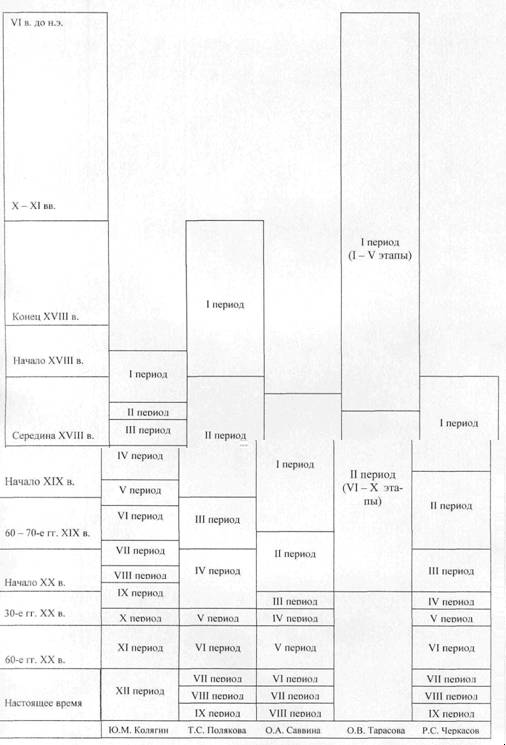
Ряд исследователей, таких как Ю.М. Колягин, Т.С. Полякова, О.А. Саввина, О.В. Тарасова, Р.С. Черкасов, в своих работах предлагают разные подходы к периодизации развития математического образования. В научных работах И.К. Андронова и Р.С. Черкасова предприняты попытки определить не только периодизацию математического образования, но и периодизацию методики преподавания математики как науки.
Так, например, Ю.М. Колягин в своем исследовании описывает развитие математического образования на фоне эволюции всей отечественной образовательной системы, в большинстве случаев обращаясь к оценке событий с государственных позиций. Это подтверждается тем, что в приложении к книге содержатся биографические сведения о деятелях науки, просвещения и культуры России в двенадцати сводных таблицах, разбитых хронологическими рамками [2]:
1. 1682 -1725 гг. (Петр I);
2. 1725 - 1740 гг. (Екатерина I, Петр II, Анна Иоановна);
3. 1741-1762 гг. (Елизавета Петровна, Петр III);
4. 1762 - 1801 гг. (Екатерина II, Павел I);
5. 1801 тАУ 1825 гг. (Александр I);
6. 1825 -1855 гг. (Николай I);
7. 1855 тАУ 1881 гг (Александр II);
8. 1881 тАУ 1894 гг. (Александр III);
9. 1894 тАУ 1918 гг. (Николай II);
10.1918 тАУ 1930 гг. (Советский период);
11.1931 тАУ 1965 гг. (Советский период);
12.1965 тАУ 1999 гг. (Советский период).
В монографии Т.С. Поляковой приводится периодизация школьного математического образования, начиная со времени Киевской Руси (X-XI вв.) и до наших дней. Она отмечает следующие этапы развития математического образования [3]:
1. Зарождение математического образования (со времени Киевской Руси (X тАУ XI вв.) тАУ XVII в.);
2. ВаСтановление отечественного математического образования (с указа Петра I об основании математико тАУ навигацкой школы (1701 г.) до 1804 г.);
3. Создание российской модели классической системы школьного математического образования (образовательные реформы 1804 г. тАУ вторая половина XIX в.);
4. Реформация классической системы школьного математического образования (60 тАУ 70-е гг. XIX в. тАУ 1917 г.);
5. Поиск новых моделей математического образования (1918 -1931 гг.);
6. Реставрация отечественных традиций, создание советской модели классического школьного математического образования (1931 тАУ 1964 гг.);
7. Реформация советской модели классической системы школьного математического образования (1964 тАУ 1982 гг.);
8. Период контрреформации (1982 тАУ 1990 гг.);
9. Современный этап развития школьного математического образования (начался с 1991 тАУ 1992 гг. и до настоящего времени).
В исследовании О.А. Саввиной определено восемь периодов становления и развития обучения высшей математике в отечественной средней школе [4]:
1. Первый период (вторая треть XVIII в. тАУ 1845 гг.) тАУ характеризуется тем, что вопросы высшей математики включались в преподавание стихийно. Обучение высшей математике в школе не носило массового характера. На данном этапе были созданы первые учебники по высшей математике на русском языке, в них формировалась лексика и терминологический аппарат понятий аналитической геометрии и анализа бесконечно малых.
2. Второй период (1846 тАУ 1906 гг.) тАУ ознаменовался стабилизацией математического образования и появлением общегосударственных программ, но вместе с тем тАУ отсутствием в программах гимназий элементов высшей математики. В этот же период ослабляются позиции аналитической геометрии в курсе кадетского корпуса (военной гимназии) и реальных училищ.
3. Третий период (1907 тАУ 1917 гг.) тАУ период Влпарадного маршаВ» элементов высшей математики в среднюю школу. В 1907 г. элементы высшей математики вошли в программу реального училища, в 1911 г. основами анализа бесконечно малых пополнился курс кадетского корпуса, а с 1914 г. сведения из аналитической геометрии заняли почетное место в программе коммерческого училища. Эти изменения не коснулись лишь классической гимназии, все попытки реформирования содержания математического образования в ней, остались только в проектах. Следует отметить, что в это время был заложен прочный фундамент методики преподавания высшей математики в средней школе (труды А.Н. Остроградского, М.Г. Попупреженко, П.А., П.А. Самохвалова, Ф.В. Филипповича, Д.М. Синцова и др.).
4. Четвертый период (1918 тАУ 1933 гг.) тАУ характеризуется тем, что Влпо инерцииВ» вопросы высшей математики, заложенные в дореволюционном курсе отдельных типов средних учебных заведений, включались в проекты программ для средней школы, но не нашли воплощения на практике.
5. Пятый период (1934 тАУ 1964 гг.) тАУ создание и функционирование советской модели классического школьного математического образования, игнорирующей элементы высшей математики на старшей ступени обучения.
6. ВаШестой период (1965 тАУ 1976 гг.) - широкая апробация элементов математического анализа в школьном курсе (в т. ч. на факультативах и математических кружках), постепенное введение элементов дифференциального и интегрального исчисления в массовую среднюю школу, поиск наиболее рациональной конструкции модели (объема, содержания и порядка изложения).
7. Седьмой период (1977 тАУ конец 80-х гг.) тАУ стабилизация содержания сведений из высшей математики в школьном курсе, период массового включения начал дифференциального и интегрального исчисления в среднюю школу, введение стабильного учебника ВлАлгебра и начала анализаВ» (под ред. А.Н. Колмогорова). Несмотря на контрреформацию содержания математического образования начала 80-х гг., элементы математического анализа в школьном курсе были сохранены. В это время создана современная методика обучения математическому анализу в средней школе (Ю.М. Колягин, Г.Л. Луканкин, Н.А. Терешин и др.).
8. Восьмой период (начало 90-х гг. по настоящее время) тАУ время поиска оптимального объема и конструкции начал математического анализа в средней школе в условиях фуркации старшей ступени школы на курсы А и В. В целом характеризуется ослаблением составляющей начал математического анализа.
В данном исследовании, предлагая именно такую модель распределения фактов истории математического образования по этапам, автор помимо закономерностей функционирования математического образования в разных социально-педагогических условиях, учитывал, в первую очередь, значение, которое придавалось высшей математике в этом процессе: изменение роли и места (ослабление или усиление) высшей математики в школьном обучении.
Таким образом, рассматриваемая периодизация, служит моделью для схематического описания генезиса обучения высшей математике в отечественной школе XVIII-XXI вв.
О.В. Тарасова выделяет два периода становления и развития геометрического образования: европейский период и русский период. Первый период (I тАУ V этапы) относится к становлению и развитию обучения геометрии в европейской школе (VI тАУ IV вв. до н.э. тАУ конец XVII века). Второй период (VI тАУ X этапы) соотносится со становлением и развитием обучения геометрии в отечественной средней школе (конец XVII века тАУ революция 1917 года) [5].
Рассмотрим эти два периода по этапам.
Первый этап (VI тАУ IV вв. до н.э.) тАУ период преобразования практической геометрии в науку теоретическую и начало обучения геометрии. Геометрия из элитной науки, доступной немногим, довольно широко распространилась, постепенно стала предметом открытого обучения. Этому способствовали различные научные школы (Фалес Милетский, Пифагор, Гиппократ Хиосский и др.)
Второй этап (начало III в. до н.э. тАУ до Рождества Христова) тАУ период возникновения научного систематического курса геометрии, благодаря написанию Евклидом ВлНачалВ» - труда, по замыслу автора, предназначенного для закрытого обучения. Тем самым была создана прочная база для дальнейших теоретических исследований (Евклид, Архимед, Аполлоний Пергский и др.).
Третий этап (I в. тАУ до конца XV в.) тАУ период начала схоластического обучения геометрии (в монастырях, городских училищах, университетах и т. п.).
Четвертый этап (начало XVI в. тАУ до конца XVI в.) тАУ период начала критики евклидовского курса в качестве школьного учебника. Создание первых курсов, ориентированных на практические начала геометрии (геодезию, черчение, предметы окружающего мира) (П. Рамус).
Пятый этап (начало XVII в. тАУ до конца XVII в.) тАУ период определения принципов первичного обучения геометрии (наглядности, доступности) (Я.А. Коменский, В. Ратихий); формирования наглядно-прикладного направления в обучении геометрии (А. Арно). Период возникновения ярких противоречий между чувственным и абстрактным в процессе усвоения геометрических знаний. Этими годами датируются первые отечественные работы по геометрии, в связи с изложением вопросов землемерия.
Далее рассмотрим второй период (русский), который начинается с шестого этапа.
Шестой этап (начало XVIII в. тАУ до середины XVIII в.) тАУ период появления в России геометрии, как учебной дисциплины, с преобладанием ее практической составляющей; появления первых российских учебников (Г.В. Крафт, Л.Ф. Магницкий и др.); закладка фундамента отечественной методической науки под влиянием иностранных ученых и педагогов (В. Христиан, Л. Эйлер и др.).
Седьмой этап (вторая половина XVIII в.) тАУ период начала массового обучения геометрии в России как самостоятельной учебной дисциплине. В это время постепенно определяется и содержание курса геометрии в различных учебных заведениях (кадетских и морских корпусах, академических гимназиях, общеобразовательных школах и т.п.). Начинается активное создание адаптированных для учащихся отечественных учебников геометрии (Д.С. Аничков, М.Е. Головин, Н.Г. Курганов, С. Назаров, С.Я. румовский и др.).
Восьмой этап (первая половина XIX века) тАУ период зарождения наглядной геометрии как составной части школьного курса геометрии; создание отечественных и переводных Влучебников для всехВ», предназначенных для сообщения начальных геометрических знаний на наглядной основе (Г. Литров, Г. Марешаль, Т.П. Татаринов и др.). В это время создаются первые отечественные систематические школьные курсы геометрии (С.Е. Гурьев, Т.Ф. Осиповский, Н.И. Фусс и др.); возникают различные методики геометрии применительно к определенному курсу (С.Е. Гурьев).
Девятый этап (вторая половина XIX века) тАУ характеризуется становлением начального и систематического курсов геометрии. В это время появляется значительное число учебников, реализующих разнообразные подходы (написанных уже более педагогически осмысленно). Появляются учебники-долгожители (А.Ю. Давидов, А.П. Киселев). Методика геометрии, изначально применительно к определенному курсу (В.Я. Буняковский, Н.И. Лобачевский, М.В. Остроградский и др.) становится методикой геометрии как раздела педагогической науки (А.Н. Остроградский). Окончательно определяется структура и содержание систематического курса, интегрирующего в себе как практические, так и теоретические основы геометрии.
Десятый этап (начало XX в. тАУ до революции 1917 г.) тАУ завершение оформления курса элементарной геометрии как самостоятельного учебного предмета, изучаемого на различных этапах школьного обучения. Создаются комплекты учебников геометрии по начальному и систематическому курсам геометрии, обеспечивающие их преемственность (Г.Я. Юревич, В.Я. Гебель и др.); создаются отдельные учебно-методические комплекты по начальному курсу геометрии (А.Р. Кулишер); формируются целостные методические теории обучения геометрии (Н.А. Извольский, С.И. Шохор-Троцкий и др.).
Таким образом, по мнению автора (Тарасовой О.В.), Влк концу рассматриваемого временного периода в отечественной средней школе сложился и оправдал себя на практике классический курс школьной геометрии, составными частями которого были курс начальной геометрии (младшее звено школы), систематический курс планиметрии (среднее звено школы) и систематический курс стереометрии (старшее звено школы). В этом курсе в органическом единстве выступали элементы теории и практики (помимо учебников существовали и задачники). К этому же времени были разработаны основы отечественной методики обучения геометрииВ» [5].
Что касается определения периодизации методики преподавания математики как науки, то И.К. Андронов в своей работе изучает зарождение, созревание, развитие, а также становление науки Влпедагогики математикиВ» и выделяет всего четыре этапа [1]:
1. Стадия зарождения предмета педагогики математики (конец XVII тАУ нач. XIX вв.);
2. Этап созревания педагогики математики, связанной с рациональным обучением математике в школе (вторая половина XIX в.);
3. Этап развития педагогики и дидактики математики (первая половина XX в.);
4. Этап становления педагогики математики, как педагогической науки (вторая половина XX в. и до наших дней).
В программной статье Р.С. Черкасова приводится периодизация в которой рассматривается не только история отечественного математического образования, но и развитие методики преподавания математики [6]:
1. Период создания первых светских школ (1700 тАУ 1800 гг.);
2. Период становления светского школьного образования. Первые научные исследования в области методики преподавания математики (1800 тАУ 1860 гг.);
3. Период развития массового среднего образования. Широкое обсуждение проблем методики преподавания математики (1860 тАУ 1900 гг.);
4. Период всероссийских съездов преподавателей математики (1900 тАУ 1917 гг.);
5. ВаПериод становления послереволюционной школы. Поиск новых путей математического образования (1918 - 1932 гг.);
6. ВаПериод совершенствования общеобразовательной трудовой политехнической школы (1932 тАУ 1964 гг.);
7. ВаПериод реформы школьного математического образования и неожиданной ее приостановки (1965 тАУ 1984 гг.);
8. ВаПериод поиска путей восстановления и развития идей реформы (1984 тАУ 1990 гг.);
9. ВаПериод современных преобразований (1990-й и последующие годы).
Несмотря на большинство совпадений, стоит обратить внимание и на некоторые различия в приведенных периодизациях.
Например, у Т.С. Поляковой, так же как и у Р.С. Черкасова, выделено девять периодов. Однако, свою периодизацию Т.С. Полякова начинает с периода зарождения математического образования Киевской Руси, а Р.С. Черкасов с создания первых светских школ (1700-1800 гг.).
Следует заметить, что согласно периодизации, предложенной Т.С. Поляковой, XVIII век относится ко второму этапу и характеризуется как этап становления математического образования.
Можно указать еще одно отличие тАУ Р.С. Черкасов в качестве самостоятельного этапа выделяет время проведения всероссийских съездов (1900 тАУ 1917 гг.), которое у Т.С. Поляковой присоединено к четвертому периоду тАУ реформации классической системы школьного математического образования (60 70-е гг. XIX в. тАУ 1917 г.).
Каждый из авторов в основу построения периодизации кладет какой-либо принцип. Так, например у Т.С. Поляковой тАУ это политика Министерства образования, его уставы, реформы; у О.А. Саввиной тАУ значение, роль и место высшей математики в процессе обучения, у О.В. Тарасовой тАУ становление и развитие геометрического образования; у Ю.М. Колягина тАУ государственные и политические интересы.
Таким образом, в этих периодизациях, имеются как общие тенденции, так и разночтения. В целях более целостного представления о развитии математического образования в России, необходимо свести все к единообразию. То есть, необходимо разработать периодизацию всего содержания математического образования, чего, к сожалению, на настоящий момент не сделано ни в одном из научных исследований.
С целью наглядности приведем сводную таблицу всех рассмотренных авторских периодизаций.
2.2 Исторические вопросы методики преподавания математики в России
Математическое образование в России находилось в 9тАФ13 веках на уровне наиболее культурных стран Восточной и Западной Европы. Затем оно было надолго задержано монгольским нашествием. В 15тАФ16 веках в связи с укреплением Русского государства и экономическим ростом страны значительно выросли потребности общества в математических знаниях. В конце 16 века и особенно в 17 веке появились многочисленные рукописные руководства по арифметике, геометрии, в которых излагались довольно обширные сведения, необходимые для практической деятельности (торговли, налогового дела, артиллерийского дела, строительства и пр.).
В Древней Руси получила распространение сходная с греко-византийской система числовых знаков, основанная на славянском алфавите. Славянская нумерация в русской математической литературе встречается до начала 18 века, но уже с конца 16 века эту нумерацию всё более вытесняет принятая ныне десятичная позиционная система.
Наиболее древнее известное нам математическое произведение относится к 1136 и принадлежит новгородскому монаху Кирику. Оно посвящено арифметико-хронологическим расчётам, которые показывают, что в то время на Руси умели решать сложную задачу вычисления пасхалий (определения на каждый год дня наступления праздника пасхи), сводящуюся в своей математической части к решению в целых числах неопределённых уравнений первой степени. Арифметические рукописи конца 16тАФ17 веков содержат, помимо описания славянской и арабской нумерации, арифметические операции с целыми положительными числами, а также под
Вместе с этим смотрят:
РЖiрархiчна структура управлiння фiзичною культурою i спортом в Хмельницькiй областi у м. КамтАЩянець-Подiльському
РЖгрова дiяльнiсть в групi продовженого дня
РЖнновацiйнi методи навчання на уроках зарубiжноi лiтератури
РЖнтенсифiкацiя навчального процесу у вищiй школi
РЖсторiя формування i розвитку форм органiзацii навчання у свiтовiй теорii та практицi